파형 (Waveform)
음성 신호는 공기를 통해 이동하는 압력 변화 ( pressure variations)로 정의되는 소리 신호다. 압력의 이러한 변화는 파동으로 설명될 수 있고 그에 따라 종종 음파 (sound waves)라고 불린다. 현재, 주로 디지털 시스템에서 그러한 파형의 분석과 처리는 항상 음향 음성 신호가 마이크에 의해 캡처되어 디지털 형태로 변환되었다고 가정할 것이다.
그런 다음 음성 신호는 시간 순간의 상대 기압을 나타내는 일련의 숫자 xn으로 표시다. 이 표현은 종종 PCM으로 약칭되는 펄스 부호 변조 (pulse code modulation)로 알려져 있다. 그런 다음 이 표현의 정확성은 두 가지 요인에 의해 지정된다.
|
샘플링 속도 (Sampling rate)
샘플링은 신호 처리의 고전적인 주제이다. 여기서 가장 중요한 측면은 나이퀴스트 주파수 (Nyquist frequency)인데, 나이퀴스트 주파수는 샘플링 속도의 절반이며 고유하게 표현할 수 있는 가장 큰 대역폭의 상단을 정의한다. 즉, 샘플링 주파수가 8000Hz라면, 0~4000Hz 주파수 범위의 신호를 이 샘플링 주파수로 고유하게 기술할 수 있다. 그런 다음 AD 컨버터는 나이퀴스트 주파수 이상의 콘텐츠를 제거하는 저역 통과 필터를 포함해야 한다.
음성 신호에서 가장 중요한 정보는 포맷 (formant)으로, 샘플링 속도의 하한이 약 7 또는 8kHz가 되도록 300Hz에서 3500Hz 범위에 존재다. 사실 AMR-NB와 같은 최초의 디지털 음성 코덱은 협대역 (narrow-band)으로 알려진 8kHz의 샘플링 속도를 사용다. 일부 자음 (consonants), 특히 마찰음 (fricatives)은 4kHz 이상의 상당한 에너지를 포함하므로 협대역은 고품질 음성에 충분하지 않다. 그러나 대부분의 에너지는 8kHz 미만으로 유지되므로 광대역, 즉 16kHz의 샘플링 속도는 대부분의 목적에 충분하다. 초광대역 (super-wide band)과 전체 대역 (full band)은 각각 32kHz와 44.1kHz (또는 48kHz)의 샘플링 속도에 더 해당다. 후자는 또한 CD (compact disk0에 사용되는 샘플링 속도이다. 이러한 더 높은 속도는 음악 및 일반 오디오와 같은 비음성 신호 (non-speech signals)를 고려할 때 유용하다.

import IPython.display as ipd
import numpy as np
import scipy
from scipy.io import wavfile
from scipy import signal
def bandpass(x,lo,hi):
X = scipy.fft.dct(x)
N = len(X)
X[0:int(lo*N*2)] = 0
X[int(hi*N*2):] = 0
return scipy.fft.idct(X)
rate,original = wavfile.read('sample.wav')
ipd.display(ipd.HTML('Original (0 to 22050 Hz)'))
ipd.display(ipd.Audio(original,rate=rate))
ipd.display(ipd.HTML('Narrowband (300 Hz to 3.3 kHz)'))
ipd.display(ipd.Audio(bandpass(original, 300/rate, 3300/rate),rate=rate))
ipd.display(ipd.HTML('Wideband (50 Hz to 7 kHz)'))
ipd.display(ipd.Audio(bandpass(original, 50/rate, 7000/rate),rate=rate))
ipd.display(ipd.HTML('Superwideband (50 Hz to 16 kHz)'))
ipd.display(ipd.Audio(bandpass(original, 50/rate, 16000/rate),rate=rate))
ipd.display(ipd.HTML('Fullband (50 Hz to 22 kHz)'))
ipd.display(ipd.Audio(bandpass(original, 50/rate, 22000/rate),rate=rate))
from ipywidgets import *
import IPython.display as ipd
import numpy as np
import scipy
from scipy.io import wavfile
from scipy import signal
import matplotlib.pyplot as plt
%matplotlib inline
filename = 'sample.wav'
fs, data = wavfile.read(filename)
data = data.astype(np.int16)
fig = plt.figure(figsize=(12, 4))
ax = fig.subplots(nrows=1,ncols=2)
t = np.arange(0.,len(data))/fs
ax[0].plot(t,data)
ax[0].set_title('Original with 16 bit accuracy and ' + str(fs/1000) + ' kHz sampling rate')
ax[1].plot(t,data)
ax[1].set_title('Original zoomed in (16 bit / ' + str(fs/1000) + ' kHz)')
ax[1].set(xlim=(0.5,0.52),ylim=(-7000,8000))
ax[0].set_xlabel('Time (s)')
ax[1].set_xlabel('Time (s)')
ax[0].set_ylabel('Amplitude')
plt.show()
import IPython.display as ipd
ipd.display(ipd.Audio(filename))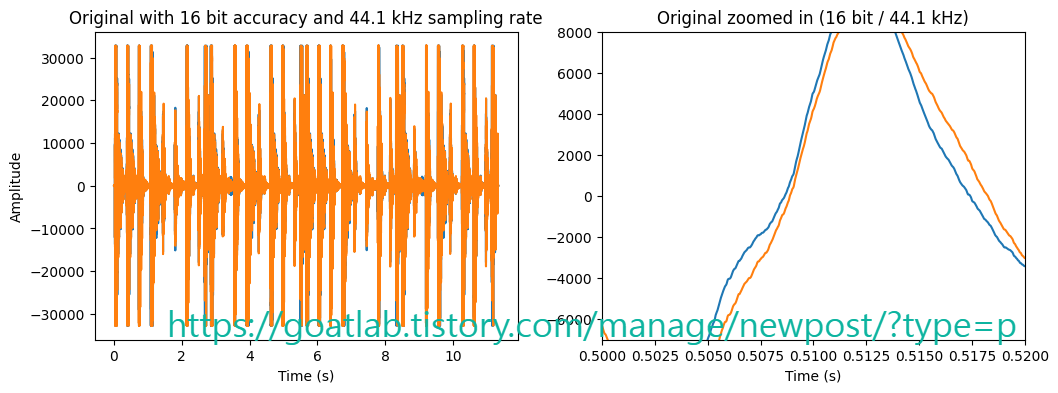
리샘플링
def update(sampling_rate=16000):
ipd.clear_output(wait=True)
resample_ratio = sampling_rate/fs
data_resample = signal.resample(data, int(len(data)*resample_ratio))
data_resample = signal.resample(data_resample, len(data))
data_resample = (data_resample*.7*(2**14)/np.max(np.abs(data_resample))).astype(np.int16)
t = np.arange(0.,len(data_resample))/fs
fig = plt.figure(figsize=(12, 4))
ax = fig.subplots(nrows=1,ncols=2)
ax[0].plot(t,data_resample)
ax[0].set_title(str(sampling_rate/1000) + ' kHz sampling rate')
ax[1].plot(t,data_resample)
ax[1].set_title('Zoom in with ' + str(sampling_rate/1000) + ' kHz')
ax[1].set(xlim=(0.5,0.52),ylim=(-7000,8000))
ax[0].set_xlabel('Time (s)')
ax[1].set_xlabel('Time (s)')
ax[0].set_ylabel('Amplitude')
plt.show()
fig.canvas.draw()
wavfile.write("sample.wav", fs, data_resample.astype(np.int16))
ipd.display(ipd.Audio('sample.wav'))
interact(update, sampling_rate=(2000, fs, 500));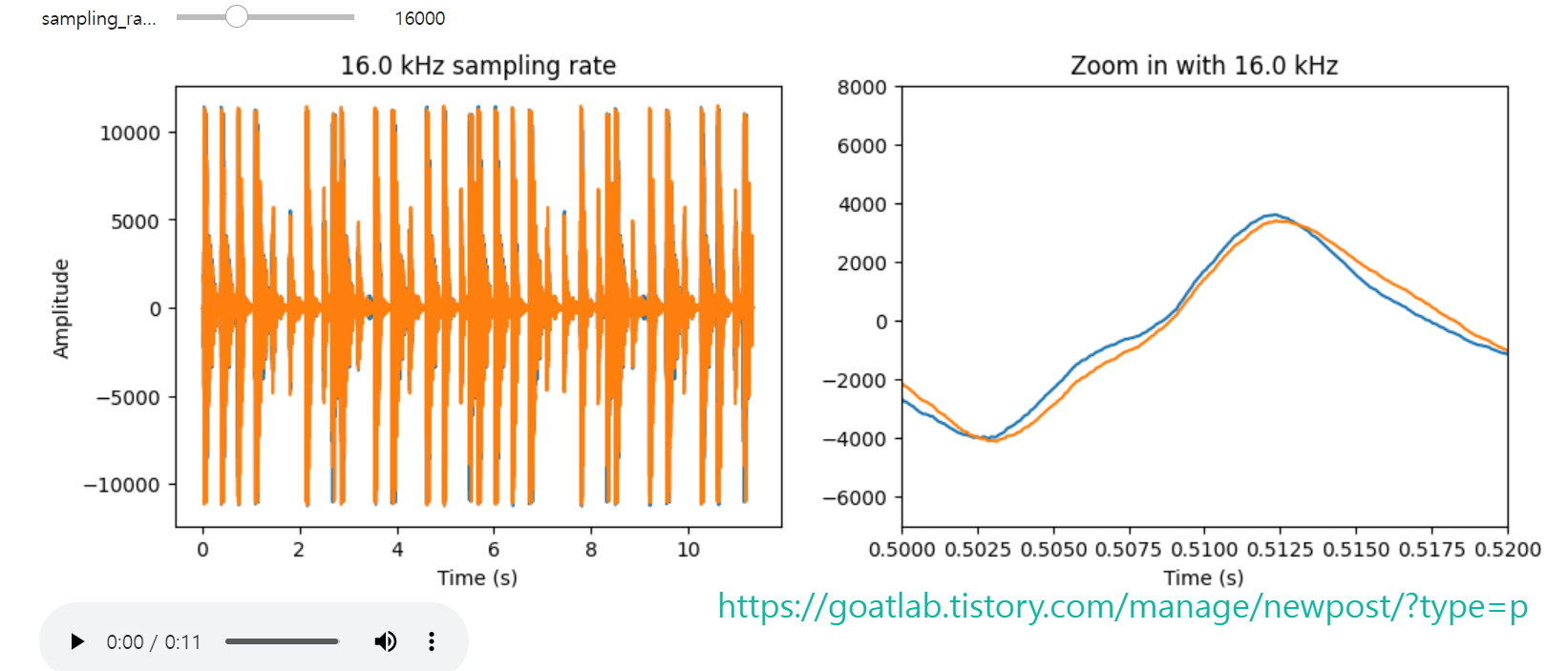
'Linguistic Intelligence > Audio Processing' 카테고리의 다른 글
| Sound Energy (0) | 2024.04.23 |
|---|---|
| 윈도우 기법 (Windowing) (0) | 2024.04.17 |
| Mel-Frequency Cepstral Coefficients (MFCC) (0) | 2024.03.20 |
| 캡스트럼 (Cepstrum) (0) | 2024.03.20 |
| 오디오 데이터 처리 (2) | 2024.03.06 |



