Mel-scale
사람 달팽이관 특성을 고려한 값을 Mel-scale이라고 한다. Mel-scale은 톤과 톤 사이의 단계가 사람이 인식하는 단계와 일치하도록 주파수를 매핑하는 척도 (scale)이다. 즉, 예를 들어 X에서 X+1 멜까지의 단계는 Y에서 Y+1 멜까지의 단계만큼 크게 들린다. 삼각형 중심이 멜 음계에서 동일한 거리 단계에 해당하는 주파수에 위치하도록 필터 뱅크 (filter bank)를 형성한다.
def freq2mel(f): return 2595*np.log10(1 + (f/700))
def mel2freq(m): return 700*(10**(m/2595) - 1)
f = np.linspace(0,8000,1000)
plt.plot(f/1000,freq2mel(f))
plt.xlabel('Frequency (kHz)')
plt.ylabel('Mel-scale')
plt.title('The mel-scale as a function of frequency')
plt.show()
melbands = 20
maxmel = freq2mel(8000)
mel_idx = np.array(np.arange(.5,melbands,1)/melbands)*maxmel
freq_idx = mel2freq(mel_idx)
melfilterbank = np.zeros((len(spectrum),melbands))
freqvec = np.arange(0,len(spectrum),1)*8000/len(spectrum)
for k in range(melbands-2):
if k>0:
upslope = (freqvec-freq_idx[k])/(freq_idx[k+1]-freq_idx[k])
else:
upslope = 1 + 0*freqvec
if k<melbands-3:
downslope = 1 - (freqvec-freq_idx[k+1])/(freq_idx[k+2]-freq_idx[k+1])
else:
downslope = 1 + 0*freqvec
triangle = np.max([0*freqvec,np.min([upslope,downslope],axis=0)],axis=0)
melfilterbank[:,k] = triangle
melreconstruct = np.matmul(np.diag(np.sum(melfilterbank**2+1e-12,axis=0)**-1),np.transpose(melfilterbank))
plt.plot(freqvec/1000,melfilterbank)
plt.xlabel('Frequency (kHz)')
plt.ylabel('Amplitude')
plt.title('The mel-filterbank')
plt.show()
#plt.plot(freqvec/1000,np.transpose(melreconstruct))
#plt.xlabel('Frequency (kHz)')
#plt.ylabel('Amplitude')
#plt.title('The mel-filterbank')
#plt.show()
# choose segment from random position in sample
starting_position = np.random.randint(total_length - window_length)
data_vector = data[starting_position:(starting_position+window_length),]
window = data_vector*windowing_function
time_vector = np.linspace(0,window_length_ms,window_length)
spectrum = scipy.fft.rfft(window,n=spectrum_length)
frequency_vector = np.linspace(0,fs/2000,len(spectrum))
# downsample to 16kHz (that is, Nyquist frequency is 8kHz, that is, everything about 8kHz can be removed)
idx = np.nonzero(frequency_vector <= 8)
frequency_vector = frequency_vector[idx]
spectrum = spectrum[idx]
logspectrum = 20*np.log10(np.abs(spectrum))
logmelspectrum = 10*np.log10(np.matmul(np.transpose(melfilterbank),np.abs(spectrum)**2)+1e-12)
logenvelopespectrum = 10*np.log10(np.matmul(np.transpose(melreconstruct),10**(logmelspectrum/10)))
plt.plot(freqvec/1000,logspectrum,label='Spectrum')
plt.plot(freqvec/1000,logenvelopespectrum,label='Mel-envelope')
plt.legend()
plt.xlabel('Frequency (kHz)')
plt.ylabel('Magnitude (dB)')
plt.title('The mel-envelope')
plt.show()


멜-포락선 (mel-envelope)은 저주파를 정확하게 모델링하며, 가장 중요한 포먼트가 있는 곳이기도 하다. 즉, 중요한 부분에 정확도가 집중되어 있어 좋다. 특히, 6.5kHz 이상의 고주파는 제대로 모델링되지 않지만 일반적으로 에너지가 너무 많지 않으므로 괜찮다.
그러나 로그 멜스펙트럼의 또 다른 문제는 인접한 샘플 간의 상관관계가 높다는 것이다. 즉, 개별 샘플 전체에 정보가 분산되어 있다는 것이다. 하지만 정확도를 더 낮출 수는 없다. 그러면 포먼트의 정확도가 떨어지기 시작하기 때문이다.
The Mel-Frequency Cepstral Coefficients
순차적으로 상관 관계가 있는 데이터를 decorrelation하는 일반적인 연산은 이산 코사인 변환 (DCT)다. 즉, 시간에 따라 상관 관계가 있는 시간 신호가 있다고 가정하면, DCT를 취하면 샘플이 상당히 상관 관계가 없는 신호의 스펙트럼을 얻을 수 있다 (적어도 입력 벡터가 고정 상태 시스템이고 긴 경우).
마찬가지로 로그-멜 스펙트럼의 DCT를 취할 수 있는데, 이를 멜-주파수 캡스트럼 계수(MFCC) 표현이라고 한다. 멜-주파수 매핑을 한 다음 로그를 취하고 마지막으로 DCT를 취한다.
MFCC는 추상적인 영역으로 시각적으로 해석하기 쉽지 않다. 하지만 크기와 주파수 축 모두 지각 (perception)과 유사하고 대략 상관 관계가 없도록 설계되었기 때문에 계산에 효율적이다.
melbands = 20
maxmel = freq2mel(8000)
mel_idx = np.array(np.arange(.5,melbands,1)/melbands)*maxmel
freq_idx = mel2freq(mel_idx)
melfilterbank = np.zeros((spectrogram.shape[1],melbands))
freqvec = np.arange(0,spectrogram.shape[1],1)*8000/spectrogram.shape[1]
for k in range(melbands-2):
if k>0:
upslope = (freqvec-freq_idx[k])/(freq_idx[k+1]-freq_idx[k])
else:
upslope = 1 + 0*freqvec
if k<melbands-3:
downslope = 1 - (freqvec-freq_idx[k+1])/(freq_idx[k+2]-freq_idx[k+1])
else:
downslope = 1 + 0*freqvec
triangle = np.max([0*freqvec,np.min([upslope,downslope],axis=0)],axis=0)
melfilterbank[:,k] = triangle
melreconstruct = np.matmul(np.diag(np.sum(melfilterbank**2+1e-12,axis=0)**-1),np.transpose(melfilterbank))
logmelspectrogram = 10*np.log10(np.matmul(np.abs(spectrogram)**2,melfilterbank)+1e-12)
mfcc = scipy.fft.dct(logmelspectrogram)
import matplotlib as mpl
default_figsize = mpl.rcParamsDefault['figure.figsize']
mpl.rcParams['figure.figsize'] = [val*2 for val in default_figsize]
mpl.rcParams['figure.figsize'] = [val*2 for val in default_figsize]
plt.imshow(20*np.log10(np.abs(np.transpose(spectrogram))+black_eps),aspect='auto',origin='lower',extent=[0, len(data)/fs,0, fs/2000])
plt.xlabel('Time (s)')
plt.ylabel('Frequency (kHz)')
plt.axis([0, len(data)/fs, 0, 8])
plt.title('Spectrogram zoomed to 8 kHz')
plt.show()
plt.imshow(np.transpose(logmelspectrogram),aspect='auto',origin='lower')
plt.xlabel('Time (s)')
#plt.ylabel('Quefrency (ms)')
#plt.axis([0, len(data)/fs, 0, 20])
plt.title('Log-mel spectrogram')
plt.show()
plt.imshow(np.transpose(mfcc),aspect='auto',origin='lower')
plt.xlabel('Time (s)')
#plt.ylabel('Quefrency (ms)')
#plt.axis([0, len(data)/fs, 0, 20])
plt.title('MFCCs over time')
plt.show()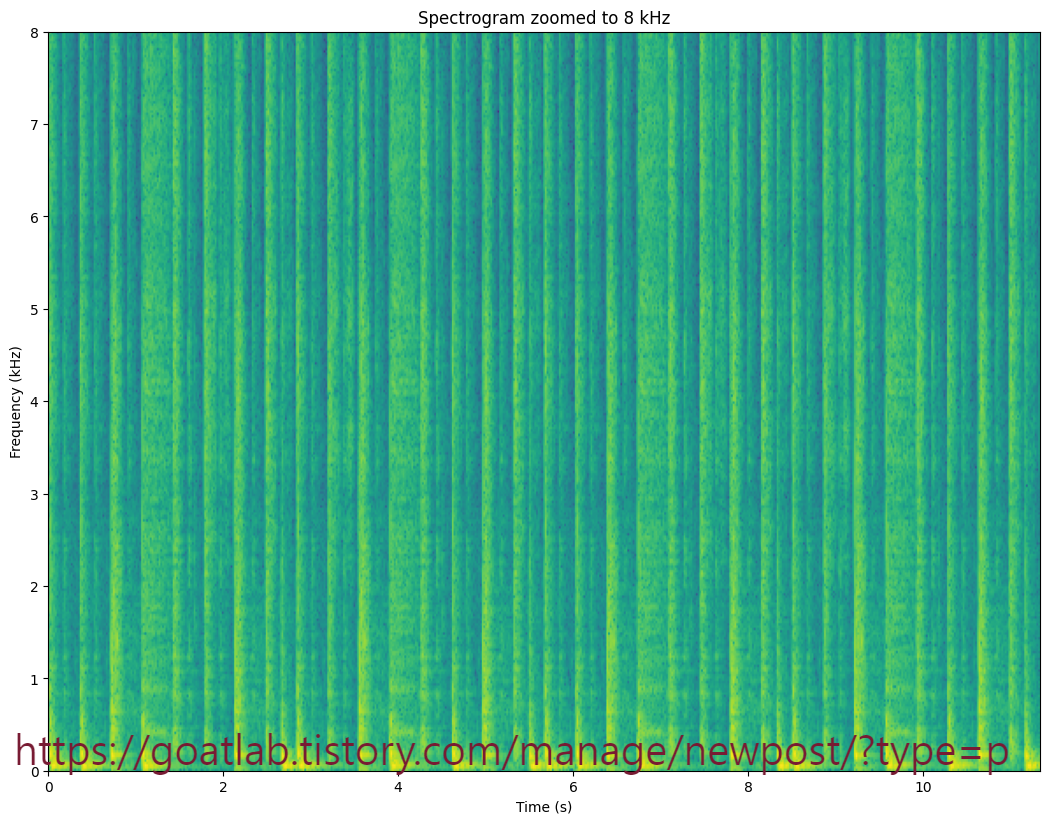
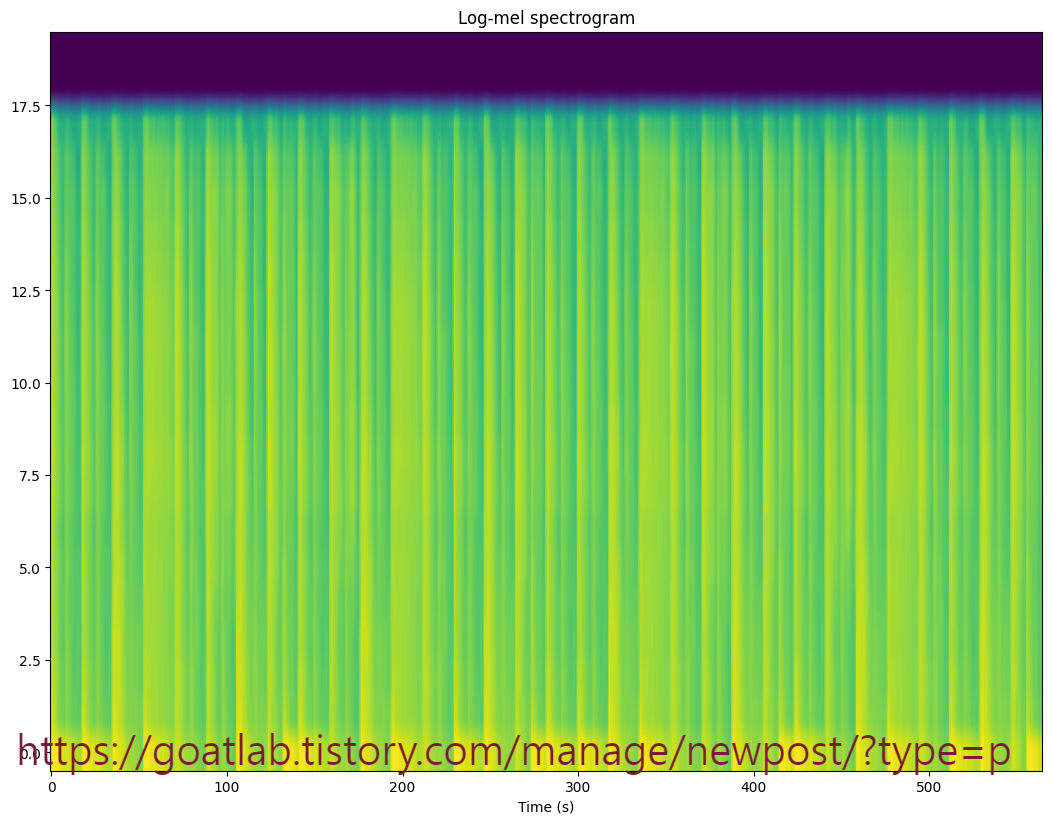
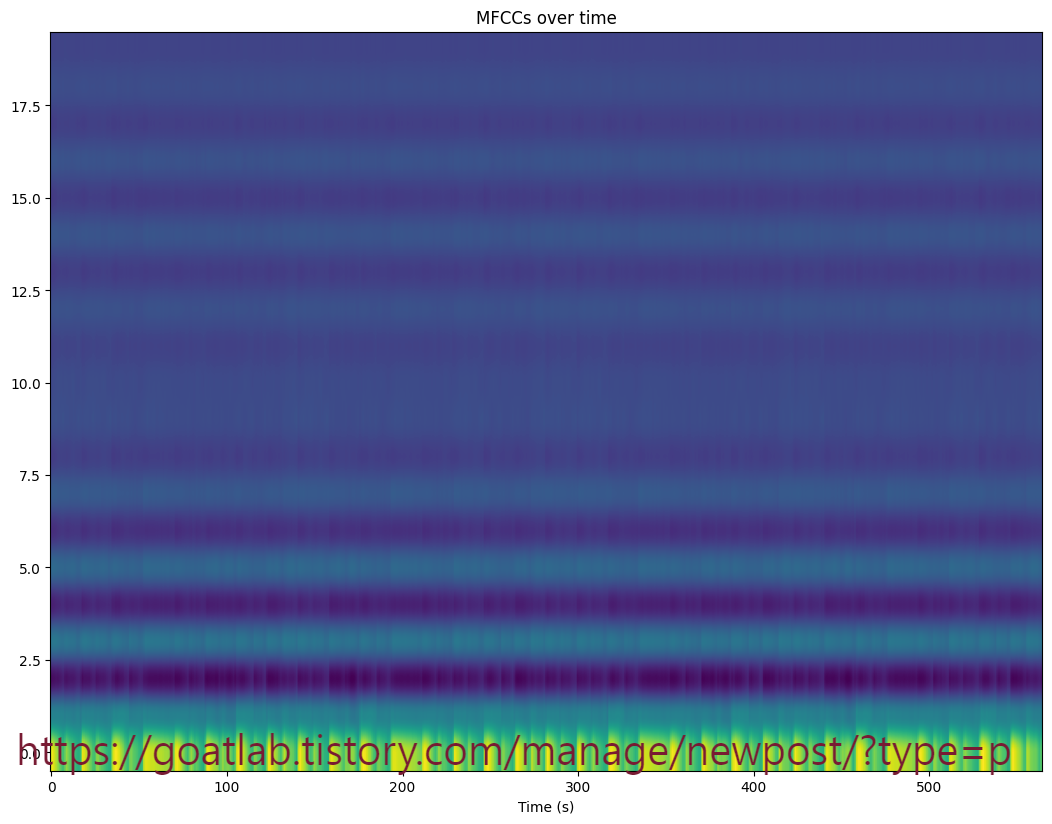
예상대로 로그 멜 스펙트로그램에서 포락선이 명확하게 보인다. MFCC도 예상대로 작동하지만 눈에 잘 띄지 않는다. 미묘한 변화를 눈에 띄게 하려면 시간이 지남에 따라 정규화해야 한다. 이러한 정규화 (pre-whitening)는 사실 머신 러닝에 입력으로 사용되는 모든 변수에 대한 표준 단계이다.
'Linguistic Intelligence > Audio Processing' 카테고리의 다른 글
| 윈도우 기법 (Windowing) (0) | 2024.04.17 |
|---|---|
| 파형 (Waveform) (0) | 2024.03.27 |
| 캡스트럼 (Cepstrum) (0) | 2024.03.20 |
| 오디오 데이터 처리 (2) | 2024.03.06 |
| 소리 및 파형 (0) | 2024.03.06 |



