배경
ICA (독립 구성 요소 분석)는 다중 채널 EEG 기록을 최대한 독립적인 구성 요소로 분해한다. 안구 활동을 나타내는 구성 요소를 식별하고 제거하여 인공물이 없는 EEG 신호를 재구성할 수 있다. 이 접근 방식은 Jung et al.에 자세히 설명되어 있다 (2000). 회귀 기반 접근 방식은 EOG 채널이 필요하지만 ICA는 참조 신호 없이 작동한다.
두 방법 모두 잠재적으로 안구 활동 외에도 뇌 활동을 제거한다. 많은 EEG 채널을 사용할 수 있는 경우 ICA는 안구 구성요소를 뇌 구성요소에서 잘 분리할 수 있다 (이를 위해서는 상대적으로 많은 데이터 샘플이 필요함). 더 깨끗한 분리는 또한 안구 구성 요소가 제거될 때 더 적은 뇌 활동이 제거됨을 의미한다. ICA 분해에 필요한 최소 EEG 채널 수는 다양하지만 경험에 따르면 최소 20개 채널이 필요한 것으로 보인다 (EEGLAB 자습서에는 ICA에 필요한 데이터 양에 대한 자세한 내용이 있다). 대조적으로 회귀 접근 방식은 몇 개의 EEG 채널만 사용할 수 있는 경우에도 작동한다. 그러나 EOG 참조 채널에는 항상 일정량의 뇌 활동이 포함되어 있으며 이는 안구 활동 외에 데이터에서도 제거된다.
ICA 방법에는 안구 구성 요소의 수동 식별이 수반되지만 이 프로세스를 자동화하는 여러 알고리즘 (ex : EyeCatch 또는 ADJUST)이 있다. 또한, ICA는 회귀 접근 방식보다 계산 시간이 더 오래 걸린다 (그러나 계산 시간을 최소로 유지하는 효율적인 구현을 사용할 수 있음). 마지막으로 ICA는 전역적으로 최적의 솔루션을 찾는 것이 보장되지 않는 최적화 문제이다. 초기 조건에 따라 알고리즘은 실행할 때마다 다른 독립 구성 요소를 찾을 수 있다. 그러나 안구 구성 요소는 분해에 걸쳐 상대적으로 안정적이기 때문에 이것은 이 응용 프로그램에서 큰 문제가 아니다.
ICA를 사용하여 MNE로 안구 인공물을 제거하는 방법을 알아보기 위해 예를 살펴본다.
데이터 전처리
회귀 접근 방식에서 이미 사용한 것과 동일한 데이터 세트를 사용한다. 특히, BNCI Horizon 2020 웹사이트 의 데이터 세트 001-2014에서 참가자 A01T를 사용한다 파일을 다운로드하여 작업 디렉토리에 저장한다. 이 데이터 세트에는 22개의 EEG 및 3개의 EOG 채널이 포함되어 있다. EOG 채널은 ICA 분해에 사용할 수 있고 사용해야 하지만 (EEG 채널과 동일한 기준 전극을 사용하는 경우), 여기서는 일을 단순하게 유지하기 위해 EEG 채널만 사용한다.
from scipy.io import loadmat
import mne
데이터는 MAT 파일로 제공되므로 SciPy의 loadmat함수를 사용하여 NumPy 배열로 로드한다. 이번에는 실제 실험 데이터가 포함된 네 번째 실행만 로드한다. 보정 실행은 필요하지 않다.
mat = loadmat("A01T.mat", simplify_cells=True)
eeg = mat["data"][3]["X"] * 1e-6 # convert to volts
두피 표면에 투영으로 ICA 구성 요소를 그린다. 이를 위해 MNE는 불행히도 데이터에 없는 채널 레이블을 알아야 한다. 그러나 데이터 설명에는 채널 이름 목록을 채우는 데 사용할 수 있는 몽타주 사진이 포함되어 있다.
ch_names = ["Fz", "FC3", "FC1", "FCz", "FC2", "FC4", "C5", "C3", "C1", "Cz",
"C2", "C4", "C6", "CP3", "CP1", "CPz", "CP2", "CP4", "P1", "Pz",
"P2", "POz", "EOG1", "EOG2", "EOG3"]
info는 목록을 사용하여 객체를 생성한다. 이 객체는 EEG 데이터 및 관련 메타 정보 (이 경우 샘플링 주파수 250Hz 및 채널 유형)를 포함하는 Raw 객체를 생성하는 데 필요하다. 마지막으로 채널 레이블을 두피의 해당 위치에 매핑하는 표준 10–20 몽타주를 추가한다. 이것은 지형도에 필요하다.
info = mne.create_info(ch_names, 250, ch_types=["eeg"] * 22 + ["eog"] * 3)
raw = mne.io.RawArray(eeg.T, info)
raw.set_montage("standard_1020")
ICA 수행
ICA는 저주파 드리프트가 있는 곳에서 작동하지 않으므로 raw 개체의 복사본을 만들고 이 복사본에 고역 통과 필터를 적용한다.
raw_tmp = raw.copy()
raw_tmp.filter(l_freq=1, h_freq=None)
이제 ICA를 수행할 준비가 되었다. 먼저, ICA객체를 인스턴스화하고 확장된 Infomax 알고리즘을 사용하도록 지정한다. picard 패키지의 방법을 사용할 수 있고 사용해야 한다. python-picard이 알고리즘은 확장된 Infomax 솔루션을 훨씬 빠르게 계산한다 (자세한 내용은 여기 참조). 어쨌든 random_state은 재현 가능한 결과를 위해 인수를 설정해야 한다.
ica = mne.preprocessing.ICA(method="infomax",
fit_params={"extended": True},
random_state=1)
다음으로 ica는 필터링된 원시 데이터에 맞춘다 (이는 22개의 EEG 채널만 사용하고 기본적으로 3개의 EOG 채널을 무시하지만 인수 raw_tmp로 변경할 수 있음).
ica.fit(raw_tmp)
안구 구성 요소 식별
이것은 일반적으로 육안 검사로 수행되므로 22개의 독립적인 구성 요소를 모두 그리는 것으로 시작한다.
ica.plot_components(inst=raw_tmp, picks=range(22))
22개의 독립적인 구성 요소가 있는 새 그림이 나타난다. 안구 구성 요소는 일반적으로 이러한 구성 요소에서 발견되기 때문에 처음 몇 가지 구성 요소에 중점을 둔다.
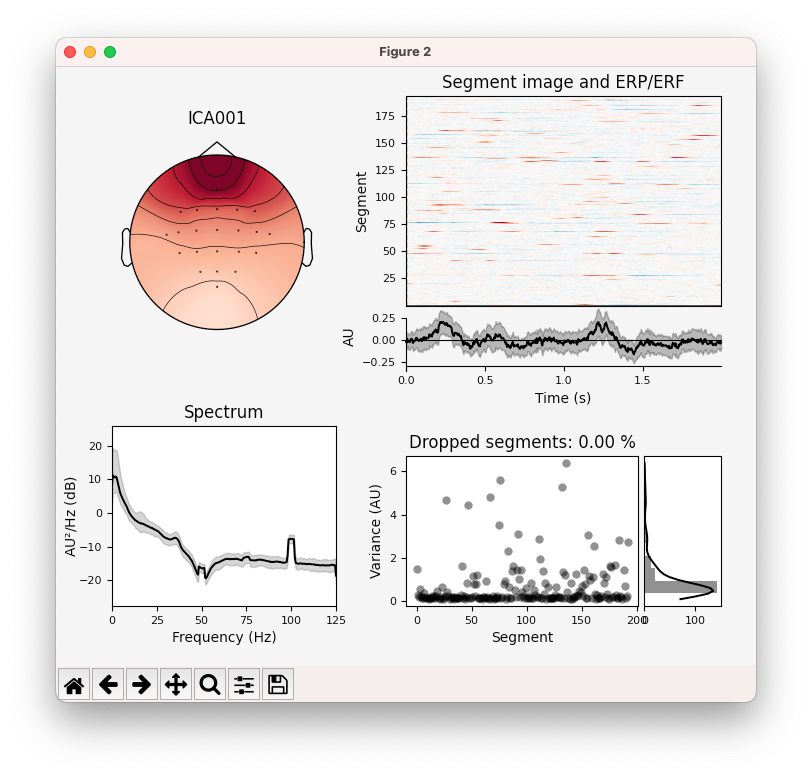
이러한 두피 투영에서 ICA001로 표시된 구성 요소 는 정면 위치 때문에 안구 운동을 나타낼 수 있는 것처럼 보인다. 확실히 하려면 이 구성 요소를 클릭하여 이 구성 요소에 대한 자세한 내용이 포함된 새 창을 열 수 있다 (inst=raw_tmp이전 호출에서 지정했기 때문에 가능). 두피 투사 (scalp projection) 외에도 검사할 수 있다.
|
요약하면, 구성 요소 ICA001이 안구 활동을 나타낸다는 것을 확신할 수 있다 . 더욱 안전하게 하기 위해 가정을 확증하기 위해 구성요소 시간 과정을 도표로 작성한다.
ica.plot_sources(inst=raw_tmp)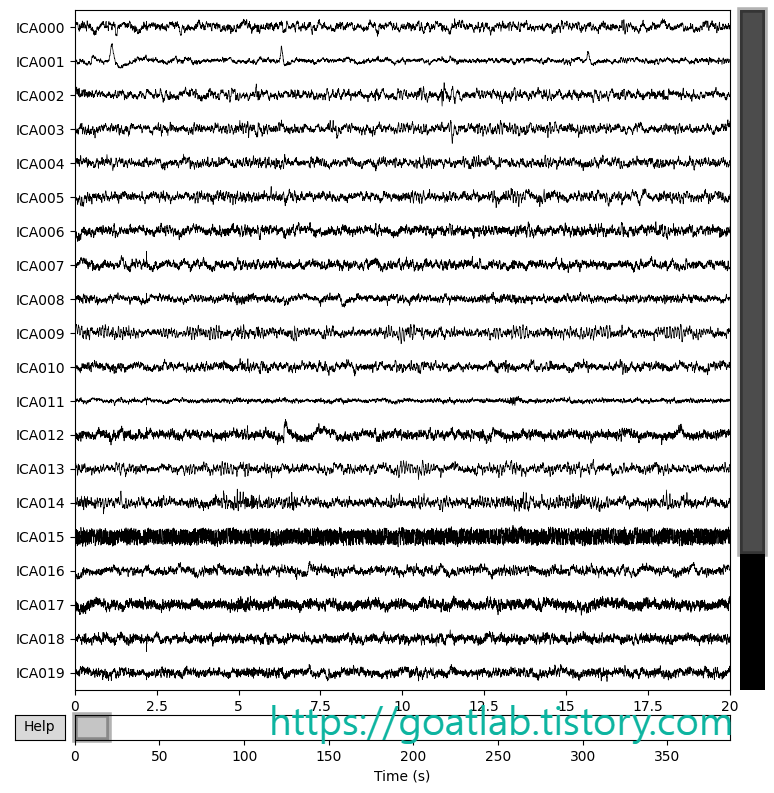
실제로 데이터를 스크롤하면 ICA001 이 주로 눈 움직임과 눈 깜박임을 캡처한다. 일반적으로 분해에서 두 개의 안구 구성 요소를 찾을 수 있지만 예제 데이터에서는 그렇지 않다 (나머지 모든 구성 요소는 눈 활동에서 비롯된 것으로 보이지 않음).
Removing ocular components
마지막 단계에서는 ica.exclude는 EEG 신호를 재구성할 때 제거해야 하는 모든 구성 요소의 인덱스를 포함하는 목록 속성을 만든다. 이 목록에는 단일 구성 요소만 포함되어 있다.
ica.exclude = [1]
생성된 ICA 구성 요소 플롯에서 구성 요소 제목 (ICA001ica.plot_components(inst=raw_tmp, picks=range(22)))을 클릭하여 구성 요소 를 포함/제외할 수 있다 (제외된 구성 요소의 제목은 회색으로 바뀜). 또한, ica.exclude는 기본 목록에서 이 구성 요소를 추가/제거한다.
이제 ICA 결과 (제외된 구성 요소 제외)를 원본 (필터링되지 않은) EEG 사본에 적용하여 아티팩트 없는 신호를 얻을 수 있다.
raw_corrected = raw.copy()
ica.apply(raw_corrected)
시각화
raw.plot(n_channels=25, start=53, duration=5, title="Before")
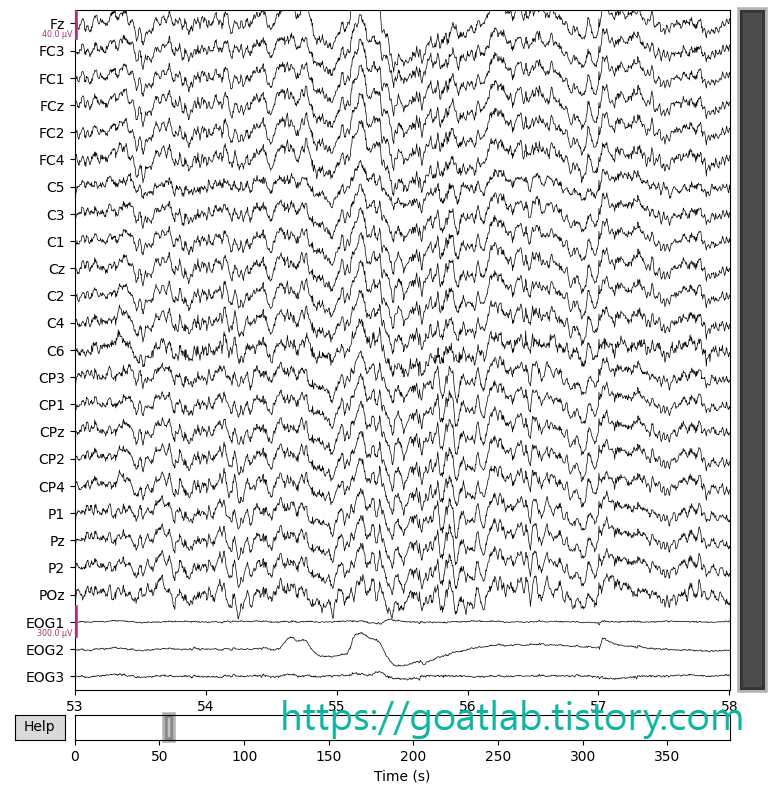
raw_corrected.plot(n_channels=25, start=53, duration=5, title="After")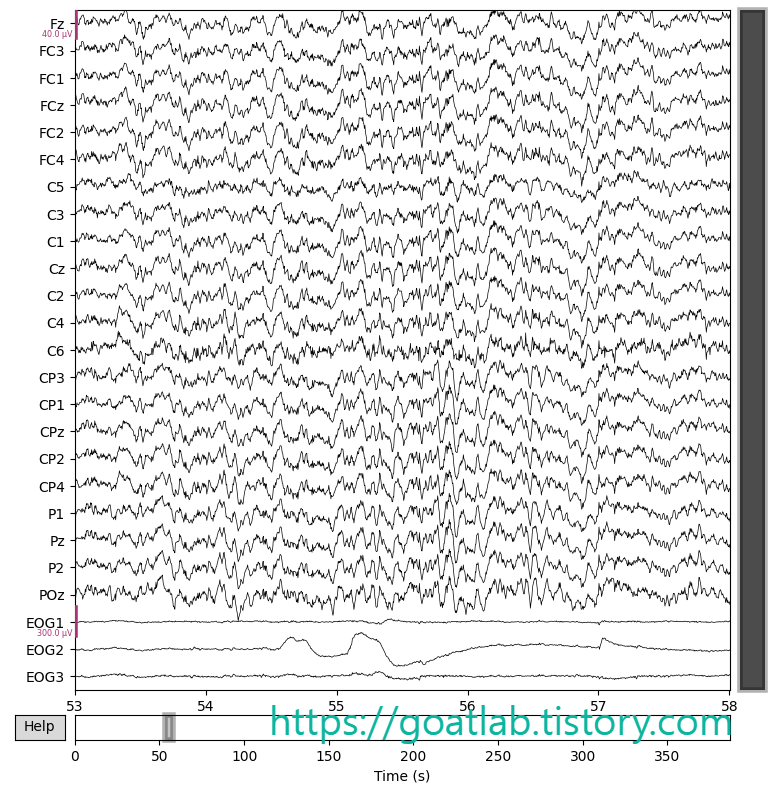
https://cbrnr.github.io/posts/removing-eog-ica/
Removing eye activity from EEG signals via ICA
EEG signals often contain eye activity (movement and/or blinks), which usually needs to be removed before performing EEG analysis. In this post, I show how to remove such ocular artifacts using independent component analysis (ICA).
cbrnr.github.io
'Brain Engineering > MNE' 카테고리의 다른 글
| [MNE-Python] 선형회귀를 이용하여 EEG 신호에서 안구 운동 제거 (0) | 2022.08.23 |
|---|---|
| 전력 스펙트럼 밀도 (Power Spectral Density) (0) | 2022.08.06 |
| Machine Learning : Classication over time (2) (0) | 2022.04.06 |
| Machine Learning : Classication over time (1) (0) | 2022.04.05 |
| Machine Learning : Group-Level Analysis (Part - 2) (3) (0) | 2022.04.05 |



