전력 스펙트럼 밀도 (Power Spectral Density)

PSD (Power Spectral Density)는 주파수 스펙트럼 (주파수 영역) 상의 전력 표현으로 신호 주파수에 따른 전력 밀도의 분포를 보기 위해 신호의 전력 대 주파수를 측정한 것이다. PSD는 일반적으로 광대역 임의 신호를 특성화하는 데 사용된다. 이는 주파수 영역에서 단위 Hz 대 주파수 당 전력의 단위로 플롯으로 볼 수 있다.

테스트 데이터
실제 PSD를 계산하기 전에 몇 가지 테스트 데이터를 생성해야 한다. 이를 위해 주파수 10Hz와 60Hz에서 두 개의 사인파를 사용한다. 또한, 신호에서 이 두 가지 주파수 구성 요소를 찾을 수 있는지 여부를 확인하기 위해 약간의 가우스 잡음을 던진다.
import numpy as np
fs = 1000.0 # 1 kHz sampling frequency
F1 = 10 # First signal component at 10 Hz
F2 = 60 # Second signal component at 60 Hz
T = 10 # 10s signal length
N0 = -10 # Noise level (dB)
t = np.r_[0:T:(1/fs)] # Sample times
# Two Sine signal components at frequencies F1 and F2.
signal = np.sin(2 * F1 * np.pi * t) + np.sin(2 * F2 * np.pi * t)
# White noise with power N0
signal += np.random.randn(len(signal)) * 10**(N0/20.0)
Scipy
이동 신호 분석 패키지 scipy에는 쉽게 사용할 수 있는 주기도를 계산하기 위한 구현이 있다 (scipy.signal.periodogram). 이를 사용하여 전력 스펙트럼 밀도를 쉽게 계산할 수 있다. periodogram 방법에 제공해야 하는 것은 실제 신호 데이터와 샘플링 주파수뿐이다. scaling='density'를 위해 메서드가 전력 스펙트럼 대신 PSD를 반환하도록 설정한다.
import scipy.signal
# f contains the frequency components
# S is the PSD
(f, S) = scipy.signal.periodogram(signal, fs, scaling='density')import matplotlib.pyplot as plt
plt.semilogy(f, S)
plt.ylim([1e-7, 1e2])
plt.xlim([0,100])
plt.xlabel('frequency [Hz]')
plt.ylabel('PSD [V**2/Hz]')
plt.show()
10Hz 및 60Hz의 해당 주파수에서 두 가지 주파수 구성 요소를 빠르게 식별할 수 있다. 둘 다 동일한 진폭을 가지므로 사인파가 동일한 진폭을 갖기 때문에 의미가 있다.
Scipy & Welch의 방법을 사용한 PSD 추정
PSD는 긴 신호를 계산하기에는 다소 무거울 수 있다. Welch의 방법은 PSD를 추정하는 잘 알려진 방법 중 하나이다. Scipy는 또한 이 추정 방법을 사용하기 위해 쉽게 사용할 수 있는 방법을 가지고 있다.
(f, S)= scipy.signal.welch(signal, fs, nperseg=1024)
plt.semilogy(f, S)
plt.xlim([0, 100])
plt.xlabel('frequency [Hz]')
plt.ylabel('PSD [V**2/Hz]')
plt.show()
Welch의 방법은 테스트 신호의 진폭 및 주파수 구성 요소에 대한 상당히 좋은 추정치를 제공한다. 노이즈에서 정확한 주파수 성분을 명확하게 식별할 수 있다.
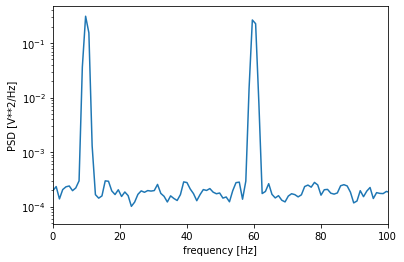
세그먼트 길이를 늘리면 더 정확한 추정치를 얻을 수 있다.
(f, S)= scipy.signal.welch(signal, fs, nperseg=4*1024)
plt.semilogy(f, S)
plt.xlim([0, 100])
plt.xlabel('frequency [Hz]')
plt.ylabel('PSD [V**2/Hz]')
plt.show()
더 긴 세그먼트 길이를 사용하면 주파수 구성요소를 더 잘 구별할 수 있다. 이것은 서로 가까운 신호 구성 요소가 있을 때 유용하다.
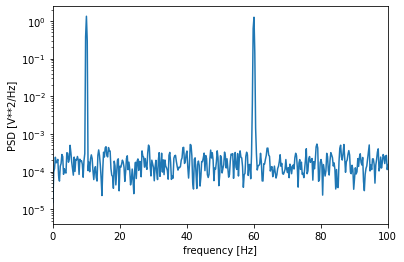
Matplotlib
Matplotlib 또한 PSD를 계산하고 플로팅하는 방법을 제공한다. 앞서 언급한 Welch의 방법을 사용하여 PSD를 계산한다.
import matplotlib.pyplot as plt
(S, f) = plt.psd(signal, Fs=fs)
plt.semilogy(f, S)
plt.xlim([0, 100])
plt.xlabel('frequency [Hz]')
plt.ylabel('PSD [V**2/Hz]')
plt.show()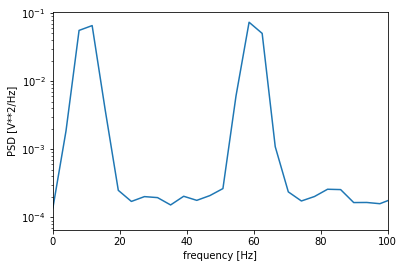
결과는 Scipy를 사용하는 Welch의 방법과 유사하다. Matplotlib를 사용하여 Scipy 종속성을 피하려면 편리할 수 있다.
Naive Python implementation
numpy 의존성만으로 구현할 수 있다. 이 구현은 정의를 직접 따르고 매우 느리다. 몇 가지 주파수에 대해서만 PSD를 계산해야 하는 경우 도움이 될 수 있다.
import numpy as np
# f is the requested frequency
# signal is the time series data
# Fs is the sampling frequency in Hz
def Sxx(f, signal, Fs):
t = 1/Fs # Sample spacing
T = len(signal) # Signal duration
s = np.sum([signal[i] * np.exp(-1j*2*np.pi*f*i*t) for i in range(T)])
return t**2 / T * np.abs(s)**2
주파수 [0,…,100]에 대한 PSD를 계산을 바로 사용할 수 있다.
# Use Sxx to calculate PSD for f in [0, 100]
S = [Sxx(f, signal, fs) for f in range(100)]
plt.semilogy([f for f in range(100)], S)
plt.xlim([0, 100])
plt.xlabel('frequency [Hz]')
plt.ylabel('PSD [V**2/Hz]')
plt.show()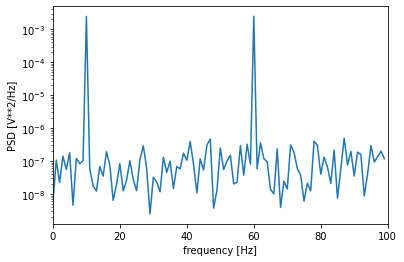
https://scicoding.com/calculating-power-spectral-density-in-python/
'Brain Engineering > MNE' 카테고리의 다른 글
| [MNE-Python] ICA를 이용하여 EEG 신호에서 안구 운동 제거 (0) | 2022.08.23 |
|---|---|
| [MNE-Python] 선형회귀를 이용하여 EEG 신호에서 안구 운동 제거 (0) | 2022.08.23 |
| Machine Learning : Classication over time (2) (0) | 2022.04.06 |
| Machine Learning : Classication over time (1) (0) | 2022.04.05 |
| Machine Learning : Group-Level Analysis (Part - 2) (3) (0) | 2022.04.05 |



