모델 구성
신경망은 층 (layer)을 쌓아서 만든다. 이 구조에서는 두 가지를 결정해야 한다.
|
이 예제의 입력 데이터는 단어 인덱스의 배열이다. 예측할 레이블은 0 또는 1이다. 이 문제에 맞는 모델을 구성한다.
# 입력 크기는 영화 리뷰 데이터셋에 적용된 어휘 사전의 크기입니다(10,000개의 단어)
vocab_size = 10000
model = keras.Sequential()
model.add(keras.layers.Embedding(vocab_size, 16, input_shape=(None,)))
model.add(keras.layers.GlobalAveragePooling1D())
model.add(keras.layers.Dense(16, activation='relu'))
model.add(keras.layers.Dense(1, activation='sigmoid'))
model.summary()
층을 순서대로 쌓아 분류기 (classifier)를 만든다.
|
은닉 유닛
위 모델에는 입력과 출력 사이에 두 개의 중간 또는 "은닉" 층이 있다. 출력 (유닛 또는 노드, 뉴런)의 개수는 층이 가진 표현 공간 (representational space)의 차원이 된다. 다른 말로, 내부 표현을 학습할 때 허용되는 네트워크 자유도의 양이다.
모델에 많은 은닉 유닛 (고차원의 표현 공간)과 층이 있다면 네트워크는 더 복잡한 표현을 학습할 수 있다. 하지만, 네트워크의 계산 비용이 많이 들고 원치않는 패턴을 학습할 수도 있다. 이런 표현은 훈련 데이터의 성능을 향상시키지만 테스트 데이터에서는 그렇지 못하다. 이를 과대적합 (overfitting)이라고 부른다.
손실 함수 / 옵티마이저
모델이 훈련하려면 손실 함수 (loss function)과 옵티마이저 (optimizer)가 필요하다. 이 예제는 이진 분류 문제이고 모델이 확률을 출력하므로 (출력층의 유닛이 하나이고 sigmoid 활성화 함수를 사용), binary_crossentropy 손실 함수를 사용한다.
다른 손실 함수를 선택할 수 없는 것은 아니다. 예를 들어, mean_squared_error를 선택할 수 있다. 하지만, 일반적으로 binary_crossentropy가 확률을 다루는데 적합하다. 이 함수는 확률 분포 간의 거리를 측정한다. 여기에서는 정답인 타깃 분포와 예측 분포 사이의 거리이다.
모델이 사용할 옵티마이저와 손실 함수를 설정한다.
model.compile(optimizer='adam',
loss='binary_crossentropy',
metrics=['accuracy'])
검증 세트 만들기
모델을 훈련할 때 모델이 만난 적 없는 데이터에서 정확도를 확인하는 것이 좋다. 원본 훈련 데이터에서 10,000개의 샘플을 떼어내어 검증 세트 (validation set)를 만든다. (테스트 세트를 사용하지 않는 이유는 훈련 데이터만을 사용하여 모델을 개발하고 튜닝하는 것이 목표이다. 그 다음 테스트 세트를 사용해서 딱 한 번만 정확도를 평가한다).
x_val = train_data[:10000]
partial_x_train = train_data[10000:]
y_val = train_labels[:10000]
partial_y_train = train_labels[10000:]
모델 훈련
이 모델을 512개의 샘플로 이루어진 미니배치 (mini-batch)에서 40번의 에포크 (epoch) 동안 훈련한다. x_train과 y_train 텐서에 있는 모든 샘플에 대해 40번 반복한다는 뜻이다. 훈련하는 동안 10,000개의 검증 세트에서 모델의 손실과 정확도를 모니터링한다.
history = model.fit(partial_x_train,
partial_y_train,
epochs=40,
batch_size=512,
validation_data=(x_val, y_val),
verbose=1)Epoch 1/40
30/30 [==============================] - 1s 18ms/step - loss: 0.6915 - accuracy: 0.5445 - val_loss: 0.6892 - val_accuracy: 0.6186
Epoch 2/40
30/30 [==============================] - 0s 10ms/step - loss: 0.6848 - accuracy: 0.7121 - val_loss: 0.6803 - val_accuracy: 0.7401
Epoch 3/40
30/30 [==============================] - 0s 10ms/step - loss: 0.6715 - accuracy: 0.7485 - val_loss: 0.6637 - val_accuracy: 0.7498
Epoch 4/40
30/30 [==============================] - 0s 10ms/step - loss: 0.6478 - accuracy: 0.7743 - val_loss: 0.6363 - val_accuracy: 0.7631
Epoch 5/40
30/30 [==============================] - 0s 11ms/step - loss: 0.6118 - accuracy: 0.7885 - val_loss: 0.5990 - val_accuracy: 0.7859
Epoch 6/40
30/30 [==============================] - 0s 11ms/step - loss: 0.5671 - accuracy: 0.8086 - val_loss: 0.5554 - val_accuracy: 0.8003
Epoch 7/40
30/30 [==============================] - 0s 11ms/step - loss: 0.5181 - accuracy: 0.8295 - val_loss: 0.5107 - val_accuracy: 0.8187
Epoch 8/40
30/30 [==============================] - 0s 11ms/step - loss: 0.4694 - accuracy: 0.8459 - val_loss: 0.4699 - val_accuracy: 0.8339
Epoch 9/40
30/30 [==============================] - 0s 10ms/step - loss: 0.4252 - accuracy: 0.8627 - val_loss: 0.4325 - val_accuracy: 0.8440
Epoch 10/40
30/30 [==============================] - 0s 11ms/step - loss: 0.3868 - accuracy: 0.8745 - val_loss: 0.4025 - val_accuracy: 0.8521
Epoch 11/40
30/30 [==============================] - 0s 11ms/step - loss: 0.3546 - accuracy: 0.8833 - val_loss: 0.3797 - val_accuracy: 0.8579
Epoch 12/40
30/30 [==============================] - 0s 10ms/step - loss: 0.3277 - accuracy: 0.8899 - val_loss: 0.3591 - val_accuracy: 0.8658
Epoch 13/40
30/30 [==============================] - 0s 10ms/step - loss: 0.3049 - accuracy: 0.8968 - val_loss: 0.3446 - val_accuracy: 0.8683
Epoch 14/40
30/30 [==============================] - 0s 10ms/step - loss: 0.2862 - accuracy: 0.9019 - val_loss: 0.3316 - val_accuracy: 0.8730
Epoch 15/40
30/30 [==============================] - 0s 10ms/step - loss: 0.2688 - accuracy: 0.9076 - val_loss: 0.3219 - val_accuracy: 0.8763
Epoch 16/40
30/30 [==============================] - 0s 10ms/step - loss: 0.2538 - accuracy: 0.9127 - val_loss: 0.3141 - val_accuracy: 0.8784
Epoch 17/40
30/30 [==============================] - 0s 11ms/step - loss: 0.2407 - accuracy: 0.9156 - val_loss: 0.3073 - val_accuracy: 0.8801
Epoch 18/40
30/30 [==============================] - 0s 11ms/step - loss: 0.2288 - accuracy: 0.9207 - val_loss: 0.3016 - val_accuracy: 0.8812
Epoch 19/40
30/30 [==============================] - 0s 11ms/step - loss: 0.2172 - accuracy: 0.9261 - val_loss: 0.2972 - val_accuracy: 0.8833
Epoch 20/40
30/30 [==============================] - 0s 11ms/step - loss: 0.2067 - accuracy: 0.9289 - val_loss: 0.2940 - val_accuracy: 0.8824
Epoch 21/40
30/30 [==============================] - 0s 11ms/step - loss: 0.1976 - accuracy: 0.9330 - val_loss: 0.2911 - val_accuracy: 0.8836
Epoch 22/40
30/30 [==============================] - 0s 11ms/step - loss: 0.1885 - accuracy: 0.9369 - val_loss: 0.2895 - val_accuracy: 0.8844
Epoch 23/40
30/30 [==============================] - 0s 11ms/step - loss: 0.1805 - accuracy: 0.9402 - val_loss: 0.2879 - val_accuracy: 0.8842
Epoch 24/40
30/30 [==============================] - 0s 11ms/step - loss: 0.1723 - accuracy: 0.9441 - val_loss: 0.2877 - val_accuracy: 0.8844
Epoch 25/40
30/30 [==============================] - 0s 10ms/step - loss: 0.1650 - accuracy: 0.9475 - val_loss: 0.2857 - val_accuracy: 0.8855
Epoch 26/40
30/30 [==============================] - 0s 10ms/step - loss: 0.1584 - accuracy: 0.9497 - val_loss: 0.2855 - val_accuracy: 0.8860
Epoch 27/40
30/30 [==============================] - 0s 10ms/step - loss: 0.1519 - accuracy: 0.9518 - val_loss: 0.2871 - val_accuracy: 0.8854
Epoch 28/40
30/30 [==============================] - 0s 10ms/step - loss: 0.1461 - accuracy: 0.9543 - val_loss: 0.2867 - val_accuracy: 0.8864
Epoch 29/40
30/30 [==============================] - 0s 10ms/step - loss: 0.1396 - accuracy: 0.9575 - val_loss: 0.2875 - val_accuracy: 0.8856
Epoch 30/40
30/30 [==============================] - 0s 10ms/step - loss: 0.1343 - accuracy: 0.9596 - val_loss: 0.2883 - val_accuracy: 0.8855
Epoch 31/40
30/30 [==============================] - 0s 10ms/step - loss: 0.1286 - accuracy: 0.9629 - val_loss: 0.2902 - val_accuracy: 0.8862
Epoch 32/40
30/30 [==============================] - 0s 11ms/step - loss: 0.1233 - accuracy: 0.9656 - val_loss: 0.2920 - val_accuracy: 0.8854
Epoch 33/40
30/30 [==============================] - 0s 11ms/step - loss: 0.1189 - accuracy: 0.9659 - val_loss: 0.2935 - val_accuracy: 0.8854
Epoch 34/40
30/30 [==============================] - 0s 11ms/step - loss: 0.1138 - accuracy: 0.9688 - val_loss: 0.2968 - val_accuracy: 0.8843
Epoch 35/40
30/30 [==============================] - 0s 11ms/step - loss: 0.1098 - accuracy: 0.9696 - val_loss: 0.2996 - val_accuracy: 0.8842
Epoch 36/40
30/30 [==============================] - 0s 11ms/step - loss: 0.1062 - accuracy: 0.9701 - val_loss: 0.3017 - val_accuracy: 0.8842
Epoch 37/40
30/30 [==============================] - 0s 11ms/step - loss: 0.1014 - accuracy: 0.9724 - val_loss: 0.3078 - val_accuracy: 0.8830
Epoch 38/40
30/30 [==============================] - 0s 11ms/step - loss: 0.0981 - accuracy: 0.9735 - val_loss: 0.3076 - val_accuracy: 0.8825
Epoch 39/40
30/30 [==============================] - 0s 10ms/step - loss: 0.0937 - accuracy: 0.9758 - val_loss: 0.3110 - val_accuracy: 0.8836
Epoch 40/40
30/30 [==============================] - 0s 10ms/step - loss: 0.0901 - accuracy: 0.9773 - val_loss: 0.3138 - val_accuracy: 0.8817
모델 평가
모델의 성능을 확인한다. 두 개의 값이 반환된다. 손실 (오차를 나타내는 숫자이므로 낮을수록 좋다)과 정확도이다.
results = model.evaluate(test_data, test_labels, verbose=2)
print(results)
782/782 - 1s - loss: 0.3335 - accuracy: 0.8722
[0.3335219919681549, 0.8722400069236755]
이 예제는 매우 단순한 방식을 사용하므로 87% 정도의 정확도를 달성했다. 고급 방법을 사용한 모델은 95%에 가까운 정확도를 얻는다.
정확도와 손실 그래프 그리기
model.fit()은 History 객체를 반환한다. 여기에는 훈련하는 동안 일어난 모든 정보가 담긴 딕셔너리 (dictionary)가 들어있다.
history_dict = history.history
history_dict.keys()
dict_keys(['loss', 'accuracy', 'val_loss', 'val_accuracy'])
네 개의 항목이 있다. 훈련과 검증 단계에서 모니터링하는 지표들이다. 훈련 손실과 검증 손실을 그래프로 그려 보고, 훈련 정확도와 검증 정확도도 그래프로 그려서 비교한다.
import matplotlib.pyplot as plt
acc = history_dict['accuracy']
val_acc = history_dict['val_accuracy']
loss = history_dict['loss']
val_loss = history_dict['val_loss']
epochs = range(1, len(acc) + 1)
# "bo"는 "파란색 점"입니다
plt.plot(epochs, loss, 'bo', label='Training loss')
# b는 "파란 실선"입니다
plt.plot(epochs, val_loss, 'b', label='Validation loss')
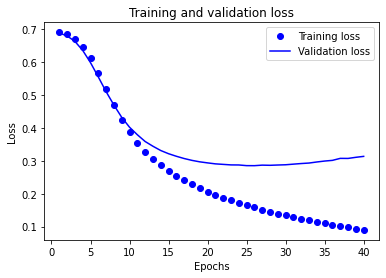
plt.title('Training and validation loss')
plt.xlabel('Epochs')
plt.ylabel('Loss')
plt.legend()
plt.show()
plt.clf() # 그림을 초기화합니다
plt.plot(epochs, acc, 'bo', label='Training acc')
plt.plot(epochs, val_acc, 'b', label='Validation acc')
plt.title('Training and validation accuracy')
plt.xlabel('Epochs')
plt.ylabel('Accuracy')
plt.legend()
plt.show()

이 그래프에서 점선은 훈련 손실과 훈련 정확도를 나타냅니다. 실선은 검증 손실과 검증 정확도입니다.
훈련 손실은 에포크마다 감소하고 훈련 정확도는 증가한다는 것을 주목해야 한다. 경사 하강법 최적화를 사용할 때 볼 수 있는 현상이다. 매 반복마다 최적화 대상의 값을 최소화한다.
하지만 검증 손실과 검증 정확도에서는 그렇지 못하다. 약 20번째 에포크 이후가 최적점인 것 같다. 이는 과대적합 때문이다. 이전에 본 적 없는 데이터보다 훈련 데이터에서 더 잘 동작한다. 이 지점부터는 모델이 과도하게 최적화되어 테스트 데이터에서 일반화되기 어려운 훈련 데이터의 특정 표현을 학습한다.
여기에서는 과대적합을 막기 위해 단순히 20번째 에포크 근처에서 훈련을 멈출 수 있다. 이것을 콜백 (callback)을 사용하여 자동으로 하는 방법이 있다.
영화 리뷰를 사용한 텍스트 분류 | TensorFlow Core
Google I/O는 끝입니다! TensorFlow 세션 확인하기 세션 보기 영화 리뷰를 사용한 텍스트 분류 Note: 이 문서는 텐서플로 커뮤니티에서 번역했습니다. 커뮤니티 번역 활동의 특성상 정확한 번역과 최신
www.tensorflow.org
'DNN with Keras > TensorFlow' 카테고리의 다른 글
| [TensorFlow] 회귀 (Regression) (2) (0) | 2022.06.15 |
|---|---|
| [TensorFlow] 회귀 (Regression) (1) (0) | 2022.06.15 |
| [TensorFlow] 기본 분류 (텍스트 분류) (1) (0) | 2022.06.15 |
| [TensorFlow] 기본 분류 (이미지 분류) (2) (0) | 2022.06.15 |
| [TensorFlow] 기본 분류 (이미지 분류) (1) (0) | 2022.06.15 |



