Linear Systems Analysis
시스템의 "입력" 자극이 시스템으로부터 "출력" 반응을 일으키는 시스템이 있다고 가정한다면, 주차장과 같은 공터에 있는 카트의 예를 생각한다. 어떤 입력 힘으로 카트를 밀면 카트는 출력 거리를 이동하게 된다. 선형 시스템은 출력이 입력에 선형적으로 의존하는 시스템으로, 즉 출력의 진폭은 입력의 진폭에 선형적으로 비례한다. 원래 힘 또는 힘의 두 배로 카트를 밀면 카트는 원래 거리의 두 배로 이동하게 된다.
선형 시스템은 시스템에 동시에 적용되는 두 개 이상의 입력에 대한 시스템의 반응을 다루는 또 다른 특성을 가지고 있다. 이 특성 (중첩이라고도 함)은 동시 입력에 대한 선형 시스템의 반응이 모든 개별 입력에 대한 시스템의 반응의 합이라고도 한다. 만약, 한 사람이 힘 p1(t)로 카트를 밀면 카트는 q1(t)로 이동하고, 다른 사람이 힘 p2(t)로 카트를 밀면 카트는 q2(t)로 이동할 것이라고 가정한다. 이제 두 사람이 동시에 힘 p1(t) + p2(t)로 카트를 밀면 카트는 q1(t) + q2(t) 미터로 이동할 것이며, 즉 각각의 푸시에 대해 카트가 이동하는 거리의 합이다.
선형 시스템의 개념을 더 잘 이해하기 위해 선형 시스템과 비선형 시스템의 대조에 초점을 맞춘다면, 비선형 시스템은 입력과 출력 사이의 관계가 비례하지 않거나 중첩되지 않는 시스템이다. 예를 들어, 주차장에서 카트를 밀고 있는 주차장에 장애물 (자동차 및 기타 카트와 같은)이 있다고 가정한다. 이 경우, 작은 힘은 카트를 특정 거리만큼 이동시킬 수 있지만, 비례적으로 큰 힘은 카트를 다른 물체와 충돌시키고 따라서 비례적으로 큰 거리를 생성하지 못할 수 있다. 이는 시스템의 복잡성으로 인해 비례성 및 중첩과 같은 단순하고 행동이 양호한 특성이 방지되는 비선형 시스템의 전형적인 예이다. 따라서, 비선형 시스템은 모델링 및 분석하기가 훨씬 더 어렵다.
몇 가지 좋은 질문은 "어디에서 선형계를 찾을 수 있는가?" 그리고 "왜 선형계가 그렇게 중요한가?"이다. 첫 번째 질문에 대한 답은 자연에서는 진정으로 선형계를 거의 마주치지 않는다는 것이다. 다시 말해서, 자연의 거의 모든 것과 인간이 만든 시스템의 모든 것은 비선형적이다. 게다가 이제 이러한 시스템의 비선형성이 그들을 매우 유연하고, 동역학적이며, 흥미롭게 만든다는 것을 안다. 첫 번째 질문에 이러한 답을 얻는다면, 두 번째 질문은 더욱 관련이 깊어질 것이다. 만약 자연에 선형계가 많지 않다면, 왜 선형계를 공부하는데 많은 시간을 써야 하는가? 답은 두 가지이다. 첫째, 많은 비선형계들은, 특정 조건 하에서, 선형 모델들로 근사화될 수 있다. 이것은 어떤 조건들이 만족되는지 확인하더라도, 복잡하고 어려운 비선형 수학을 다루는 대신, 간단한 선형 수학을 여전히 사용할 수 있다는 것을 의미한다. 둘째, 선형 모델들이 진정으로 비선형적인 시스템의 종류와 성질에 대한 지식이 부족한 경우에도, 선형 모델이 할 수 있는 전부일 수 있다. 예를 들어, 사람이 많은 주차장에서 카트를 밀고 있는 모델에서, 비록 그 시스템이 비선형적이라고 할지라도, 적용된 힘을 제한한다면, 여전히 시스템을 선형 시스템으로 모델화할 수 있다.
선형 시스템의 분석을 위해 FT가 선형계에 미치는 영향을 확인하다. 이를 위해서는 입력 p(t), 출력 q(t), 그리고 선형계 h(t)의 내부 특성 사이의 관계를 설명하는 것으로 충분하다. 출력은 입력과 모델의 내부 특성 사이의 컨볼루션에 지나지 않는다.

컨볼루션은 다소 복잡한 과정이지만 FT를 사용하여 선형 시스템의 출력을 쉽게 계산할 수 있다.
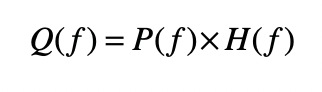
h(t) (또는 동등하게 H(f))의 개념을 충격 함수와 관련시키는 것이 있다.

입력이 충격이라고 가정하면, p(t) = π(t)이다.

h(t) = q(t)를 얻는다. 이는 선형 시스템의 내부 특성을 찾기 위해 단순히 시스템에 임펄스 입력을 인가하여 출력을 기록하면 된다는 것을 의미하며, 이러한 임펄스 함수의 특성은 시스템 식별 및 신호 처리에 사용되며, 이러한 관측으로 인해 h(t)는 종종 "임펄스 응답 함수"라고 불린다.
Differentiation
FT의 또 다른 흥미로운 성질은 시간 영역에서의 도함수를 주파수 영역에서의 단순 곱셈 과정으로 변환하는 것이다. 이 성질은 시간의 미분방정식을 주파수 영역에서의 단순 선형 방정식의 집합으로 변환하고 단순 선형대수를 이용하여 다차원 미분방정식을 푸는 데 사용된다.
Scaling Property
FT의 매우 유용한 특성은 시간과 주파수 영역이 역스케일링되는 방식이다. 구체적으로, 신호 g(t)의 FT가 G(f)로 주어진다고 가정하면, 스케일링 특성은 α > 1인 g1(t) = g(αt)로 정의된 신호에 대해 다음과 같이 G(f)를 사용하여 FT를 쉽게 계산할 수 있음을 나타낸다.

방정식은 일단 함수가 시간적으로 압축되면 주파수 영역의 함수는 동일한 속도로 확장된다는 것을 주장한다. 이것은 시간 영역의 신호의 폭이 0에 가까워지면 주파수 영역의 폭이 무한대에 가까워진다는 것을 의미한다. 이 관찰은 충격 함수의 FT가 무한대로 평평해야 하는 이유를 더 설명한다.
'Signal Processing > Fourier Transform' 카테고리의 다른 글
| FFT (Fast Fourier Transform) vs STFT (Short-Time Fourier Transform) (0) | 2023.10.02 |
|---|---|
| [Fourier Transform] 1차원 푸리에 변환의 특성 (1) (0) | 2023.07.31 |
| 푸리에 변환 (Fourier Transform) (0) | 2023.07.31 |


