728x90
반응형
SMALL
Estimating the Coefficient of the AR Model
계수 a(1), ..., a(p) 및 모형 순서 p를 결정해야 한다. 계수의 추정은 p 미지의 p 방정식의 동시 해를 포함한다. 표본 x(k)의 예측은 이전 표본의 수 p, x(k-1), ..., x(k-p)로부터 도출된다.
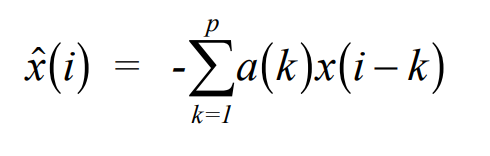
n(i)이라는 용어는 시간 i에서 시계열의 실제 값과 자기 회귀에 의해 결정되는 값 사이의 차이이기 때문에 예측의 오류로 볼 수 있다. 예측 오차 또는 잔차 e(i)를 x(i)의 추정치가 실제 값에서 벗어나는 것으로 정의한다.
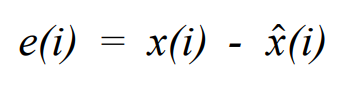
모형 계수의 최적 값은 예측 오차 e(i)의 절대값을 최소화하는 값이다. e(i)의 제곱값을 최소화함으로써 이것을 달성할 수 있다. 오차 제곱을 최소화하는 계수의 최선의 추정치를 찾기 위해 사용 가능한 모든 N개 시점의 평균 오차를 최소화한다. 이를 평균 제곱 오차 최소화 (MSE)라고 한다.

a(k)에 대한 최소화는 0과 동일한 (k)에 대한 MSE의 부분 도함수를 설정하는 것을 포함한다.

이것은 Yule-Walker 방정식이라고 불린다.
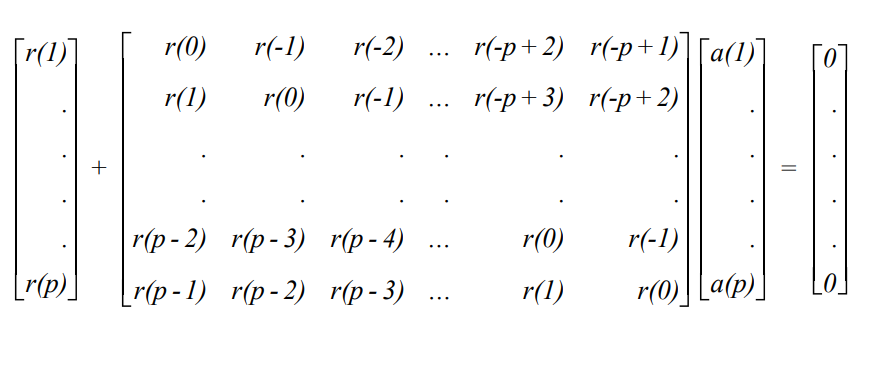
compact 매트릭스 형식은
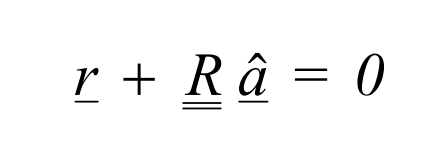
여기서 R은 자기공분산 행렬이다.
728x90
반응형
LIST
'Signal Processing' 카테고리의 다른 글
| Use of AR Models to Estimate Spectra (0) | 2022.04.13 |
|---|---|
| AR Model Order Estimation (0) | 2022.04.13 |
| AR (Autoregressive) Burg Method (0) | 2022.04.13 |
| 스펙트로그램 (Spectrogram) (0) | 2022.04.12 |
| ICA (Independent components analysis) (0) | 2022.04.11 |



