Mean Error
MSE, MAE 및 RMSE는 회귀 분석에서 예측 오류율과 모델 성능을 평가하는 데 주로 사용된다.
MAE (Mean Absolute Error)

MAE (평균 절대 오차)는 데이터 세트에 대한 평균 절대 차이에 의해 추출된 원래 값과 예측 값 사이의 차이를 나타낸다.
from sklearn.metrics import median_absolute_error
y_true = [3, 5, 7]
y_pred = [0, 4, 9]
median_absolute_error(y_true, y_pred)2.0
MSE (Mean Squared Error)

MSE (평균 제곱 오차)는 데이터 집합에 대한 평균 차이를 제곱하여 추출한 원래 값과 예측 값의 차이를 나타낸다.
from sklearn.metrics import mean_squared_error
y_true = [3, 5, 7]
y_pred = [0, 4, 9]
mean_squared_error(y_true, y_pred)4.666666666666667
RMSE (Root Mean Squared Error)

RMSE (Root Mean Squared Error)는 MSE의 제곱근에 의한 오류율이다.
import math
from sklearn.metrics import mean_squared_error
y_true = [3, 5, 7]
y_pred = [0, 4, 9]
math.sqrt(mean_squared_error(y_true, y_pred))2.160246899469287
결정 계수 (R-squared)

결정 계수는 회귀 모형에서 독립 변수에 의해 설명되는 종속 변수에 대한 분산의 비율을 나타내는 통계적 측도를 말한다. 두 개의 값의 증감이 얼마나 일관성을 가지는지 나타내는 지표이며, 0에서 1사이의 값인 1에 가까울수록 모델이 해당 데이터에 대한 높은 연관성을 가진다.
from sklearn.metrics import r2_score
y_true = [3, -0.5, 2, 7]
y_pred = [2.5, 0.0, 2, 8]
r2_score(y_true, y_pred)0.9486081370449679
피어슨 상관 계수 (Pearson Correlation Coefficient, PCC)

통계학에서 , 피어슨 상관 계수 (Pearson Correlation Coefficient, PCC)란 두 변수 X 와 Y 간의 선형 상관 관계를 계량화한 수치다. 피어슨 상관 계수는 코시-슈바르츠 부등식에 의해 +1과 -1 사이의 값을 가지며, +1은 완벽한 양의 선형 상관 관계, 0은 선형 상관 관계 없음, -1은 완벽한 음의 선형 상관 관계를 의미한다. 일반적으로 상관관계는 피어슨 상관관계를 의미하는 상관계수이다.
스피어먼 상관 계수 (Spearman rank-order correlation coefficient, SROCC)
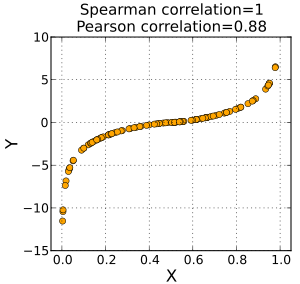
통계에서 스피어먼 상관 계수는 두 변수의 순위 사이의 통계적 의존성을 측정하는 비모수적인 척도이다. 이는 두 변수의 관계가 단조함수 (單調函數,monotonic function)를 사용하여 얼마나 잘 설명될 수 있는지를 평가한다.
두 변수 간의 스피어먼 상관 계수는 두 변수의 순위 값 사이의 피어슨 상관 계수와 같다. 따라서, 칼 피어슨의 상관 계수가 두 변수 사이의 선형 관계를 평가하는 반면 찰스 스피어먼의 상관 계수는 단조 적 관계 (선형인지 여부는 아님)를 평가한다. 중복 데이터 값이 없으면 각 변수가 다른 변수의 완벽한 단조 함수 일 때 +1 또는 -1의 완벽한 스피어만 상관 관계가 발생한다.
'AI-driven Methodology > Artificial Intelligence' 카테고리의 다른 글
| [AI] 평가 모델 (2) (0) | 2022.09.27 |
|---|---|
| [AI] 평가 모델 (1) (0) | 2022.09.27 |
| [AI] 인공지능의 역사 (주요 응용 분야) (4) (0) | 2022.09.17 |
| [AI] 인공지능의 역사 (3) (0) | 2022.09.17 |
| [AI] 인공지능의 역사 (2) (0) | 2022.09.15 |



