728x90
반응형
SMALL
수치 미분 (Numerical Derivative)
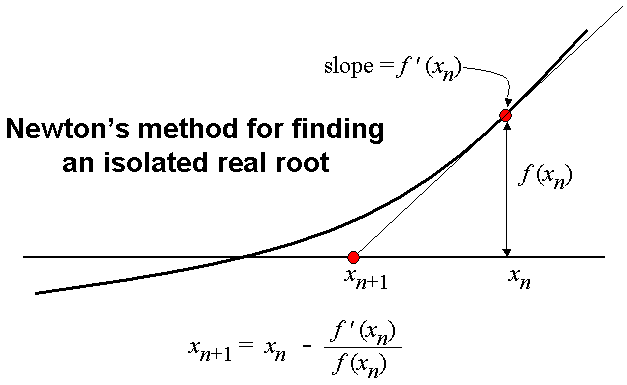
데이터 관점에서 미분은 loss를 줄이기 위해 x를 조금씩 변화시키는 것이다.
import numpy as np
# 미분 함수
def numerical_derivative(f, x):
delta_x = 1e-4
grad = np.zeros_like(x)
it = np.nditer(x, flags=['multi_index'], op_flags=['readwrite'])
while not it.finished:
idx = it.multi_index
tmp_val = x[idx]
x[idx] = float(tmp_val) + delta_x
fx1 = f(x) # f(x+delta_x)
x[idx] = float(tmp_val) - delta_x
fx2 = f(x) # f(x-delta_x)
grad[idx] = (fx1 - fx2) / (2*delta_x)
x[idx] = tmp_val
it.iternext()
return grad# 입력 변수 1개인 함수 f(x) = x^2
def func1(input_obj):
x = input_obj[0]
return x**2
# 입력 변수 2개인 함수 f(x, y) = x + 2xy + y^3
def func2(input_obj):
x = input_obj[0]
y = input_obj[1]
return (x + 2*x*y + np.power(y, 3))
# 입력변수 4 개인 함수 f(w,x,y,z) = wx + xyz + 3w + zy^2
def func3(input_data):
w = input_data[0, 0]
x = input_data[0, 1]
y = input_data[1, 0]
z = input_data[1, 1]
return ( w*x + x*y*z + 3*w + z*np.power(y,2) )input = np.array([1.0, 2.0])
# 입력을 2X2 행렬로 구성함
input_data = np.array([[1.0, 2.0], [3.0, 4.0]])
# lambda function 정의
f = lambda W : func3(W)
ret = numerical_derivative(f, input_data)
print(numerical_derivative(func1, np.array([3.0])))
print(numerical_derivative(func2, input)
print(ret)
선형 회귀 (Linear Regression)
선형 회귀는 종속 변수 y와 한 개 이상의 독립 변수 x와의 선형 상관 관계를 모델링하는 회귀분석 기법이다. 한 개의 설명 변수에 기반한 경우에는 단순 선형 회귀, 둘 이상의 설명 변수에 기반한 경우에는 다중 선형 회귀라고 한다.
Data Definition
import numpy as np
from datetime import datetime
loaded_data = np.loadtxt('./sps.csv', delimiter=',', dtype=np.float32)
x_data = loaded_data[ :, 1:]
t_data = loaded_data[ :, [0]]
# 데이터 차원 및 shape 확인
print("loaded_data.ndim = ", loaded_data.ndim, ", loaded_data.shape = ", loaded_data.shape)
print("x_data.ndim = ", x_data.ndim, ", x_data.shape = ", x_data.shape)
print("t_data.ndim = ", t_data.ndim, ", t_data.shape = ", t_data.shape)loaded_data.ndim = 2 , loaded_data.shape = (50, 5)
x_data.ndim = 2 , x_data.shape = (50, 4)
t_data.ndim = 2 , t_data.shape = (50, 1)
Initialize Weights and Bias
np.random.seed(0)
W = np.random.rand(4,1) # 4X1 행렬 (입력 데이터의 개수만큼)
b = np.random.rand(1)
print("W = ", W, ", W.shape = ", W.shape, ", b = ", b, ", b.shape = ", b.shape)W = [[0.5488135 ]
[0.71518937]
[0.60276338]
[0.54488318]] , W.shape = (4, 1) , b = [0.4236548] , b.shape = (1,)
Define Loss Function and Output (y)
def loss_func(x, t):
y = np.dot(x,W) + b
return ( np.sum( (t - y)**2 ) ) / ( len(x) )
def numerical_derivative(f, x):
delta_x = 1e-4 # 0.0001
grad = np.zeros_like(x)
it = np.nditer(x, flags=['multi_index'], op_flags=['readwrite'])
while not it.finished:
idx = it.multi_index
tmp_val = x[idx]
x[idx] = float(tmp_val) + delta_x
fx1 = f(x) # f(x+delta_x)
x[idx] = float(tmp_val) - delta_x
fx2 = f(x) # f(x-delta_x)
grad[idx] = (fx1 - fx2) / (2*delta_x)
x[idx] = tmp_val
it.iternext()
return grad
# 손실함수 값 계산 함수
# 입력변수 x, t : numpy type
def error_val(x, t):
y = np.dot(x,W) + b
return ( np.sum( (t - y)**2 ) ) / ( len(x) )
Learning
learning_rate = 1e-4
f = lambda x : loss_func(x_data,t_data)
print("Initial error value = ", error_val(x_data, t_data), "Initial W = ", W, "\n", ", b = ", b )
start_time = datetime.now()
for step in range(30001): # 3만번 반복수행
W -= learning_rate * numerical_derivative(f, W)
b -= learning_rate * numerical_derivative(f, b)
if (step % 500 == 0):
print("step = ", step, "error value = ", error_val(x_data, t_data) )
end_time = datetime.now()
print("")
print("Elapsed Time => ", end_time - start_time)Output exceeds the size limit. Open the full output data in a text editor
Initial error value = 64.38302549674624 Initial W = [[0.5488135 ]
[0.71518937]
[0.60276338]
[0.54488318]]
, b = [0.4236548]
step = 0 error value = 60.604776072341444
step = 500 error value = 0.01167190429026227
step = 1000 error value = 0.004047845907167936
step = 1500 error value = 0.0014043526649038332
step = 2000 error value = 0.00048722369128301977
step = 2500 error value = 0.00016903654707396402
step = 3000 error value = 5.864524808192556e-05
step = 3500 error value = 2.0346281216250795e-05
step = 4000 error value = 7.0589037112171215e-06
step = 4500 error value = 2.4490038781355694e-06
step = 5000 error value = 8.496531813563435e-07
step = 5500 error value = 2.9477720922949027e-07
step = 6000 error value = 1.0226949652836696e-07
step = 6500 error value = 3.5481202727676135e-08
step = 7000 error value = 1.230978727513882e-08
step = 7500 error value = 4.2707363649495105e-09
step = 8000 error value = 1.4816819081469759e-09
step = 8500 error value = 5.14052165565946e-10
step = 9000 error value = 1.7834437166114527e-10
step = 9500 error value = 6.187448869478846e-11
...
step = 29500 error value = 7.812023703927484e-28
step = 30000 error value = 7.296706880293302e-28
Elapsed Time => 0:00:06.304803print(W)
print(b)[[ 1.]
[-1.]
[ 1.]
[-1.]]
[2.38435128e-14]
Evaluate and Predict
# 학습을 마친 후, 임의의 데이터에 대해 미래 값 예측 함수
# 입력변수 x : numpy type
def predict(x):
y = np.dot(x,W) + b
return yex_data_01 = np.array([4, 4, 4, 4]) # 4 - 4 + 4 - 4 = 0
print("predicted value = ", predict(ex_data_01) )predicted value = [-3.21117277e-14]
728x90
반응형
LIST
'AI-driven Methodology > Artificial Intelligence' 카테고리의 다른 글
| [AI] Feed Forward ∙ One Hot Encoding ∙ Softmax (0) | 2022.07.17 |
|---|---|
| [AI] 로지스틱 회귀 (Logistic Regression) (0) | 2022.07.10 |
| [AI] 러닝 아키텍처 (0) | 2022.07.09 |
| [AI] 인공지능 ∙ 머신러닝 ∙ 딥러닝 (0) | 2022.07.09 |
| 인공지능 기술 (0) | 2022.07.09 |



