나이브 베이즈 (Naive Bayes)

나이브 베이즈는 분류기를 만들 수 있는 간단한 기술로써 단일 알고리즘을 통한 훈련이 아닌 일반적인 원칙에 근거한 여러 알고리즘들을 이용하여 훈련된다. 모든 나이브 베이즈 분류기는 공통적으로 모든 특성 값은 서로 독립임을 가정한다. 예를 들어, 특정 과일을 사과로 분류 가능하게 하는 특성들 (둥글다, 빨갛다, 지름 10cm)은 나이브 베이즈 분류기에서 특성들 사이에서 발생할 수 있는 연관성이 없음을 가정하고 각각의 특성들이 특정 과일이 사과일 확률에 독립적으로 기여 하는 것으로 간주한다.
나이브 베이즈의 장점은 다음과 같다. 첫째, 일부의 확률 모델에서 나이브 베이즈 분류는 지도 학습 (Supervised Learning) 환경에서 매우 효율적으로 훈련 될 수 있다. 많은 실제 응용에서, 나이브 베이즈 모델의 파라미터 추정은 최대우도방법 (Maximum Likelihood Estimation ; MLE)을 사용하며, 베이즈 확률론이나 베이지안 방법들은 이용하지 않고도 훈련이 가능하다. 둘째, 분류에 필요한 파라미터를 추정하기 위한 트레이닝 데이터의 양이 매우 적다는 것이다. 셋째, 간단한 디자인과 단순한 가정에도 불구하고, 나이브 베이즈 분류는 많은 복잡한 실제 상황에서 잘 작동한다.
조건부독립
확률변수 A, B가 독립이면 A, B의 결합확률은 주변확률의 곱과 같다.
조건부독립 (conditional independence)은 일반적인 독립과 달리 조건이 되는 별개의 확률변수 C가 존재해야 한다. 조건이 되는 확률변수 C에 대한 A, B의 결합조건부확률이 C에 대한 A, B의 조건부확률의 곱과 같으면 A와 B가 C에 대해 조건부독립이라고 한다.
$$ 𝑃(𝐴,𝐵|𝐶)=𝑃(𝐴|𝐶)𝑃(𝐵|𝐶)$$기호로는 다음과 같이 표기한다.
$$ 𝐴⫫𝐵|𝐶 $$조건부독립과 비교하여 일반적인 독립은 무조건부독립이라고 한다. 무조건부독립은 다음과 같이 표기하도 한다.
A, B가 C에 대해 조건부독립이면 다음도 만족한다.
$$ 𝑃(𝐴|𝐵,𝐶)=𝑃(𝐴|𝐶) $$ $$ 𝑃(𝐵|𝐴,𝐶)=𝑃(𝐵|𝐶) $$주의할 점은 조건부독립과 무조건부독립은 관계가 없다는 점이다. 즉, 두 확률변수가 독립이라고 항상 조건부독립이 되는 것도 아니고 조건부독립이라고 꼭 독립이 되는 것도 아니다.
$$ 𝑃(𝐴,𝐵)=𝑃(𝐴)𝑃(𝐵)\bcancel⟹𝑃(𝐴,𝐵|𝐶)=𝑃(𝐴|𝐶)𝑃(𝐵|𝐶) $$ $$ 𝑃(𝐴,𝐵|𝐶)=𝑃(𝐴|𝐶)𝑃(𝐵|𝐶)\bcancel⟹𝑃(𝐴,𝐵)=𝑃(𝐴)𝑃(𝐵) $$
np.random.seed(0)
C = np.random.normal(100, 15, 2000)
A = C + np.random.normal(0, 5, 2000)
B = C + np.random.normal(0, 5, 2000)
plt.figure(figsize=(8, 4))
plt.subplot(121)
plt.scatter(A, B)
plt.xlabel("A")
plt.ylabel("B")
plt.xlim(30, 180)
plt.ylim(30, 180)
plt.title("B와 C의 무조건부 상관관계")
plt.subplot(122)
idx1 = (118 < C) & (C < 122)
idx2 = (78 < C) & (C < 82)
plt.scatter(A[idx1], B[idx1], label="C=120")
plt.scatter(A[idx2], B[idx2], label="C=80")
plt.xlabel("A")
plt.ylabel("B")
plt.xlim(30, 180)
plt.ylim(30, 180)
plt.legend()
plt.title("B와 C의 조건부 상관관계")
plt.tight_layout()
plt.show()
나이브 가정
독립변수 𝑥가 𝐷차원이라고 가정하자.
가능도함수는 𝑥1,…,𝑥𝐷의 결합확률이 된다.
원리상으로는 𝑦=𝑘인 데이터만 모아서 이 가능도함수의 모양을 추정할 수 있다. 하지만 차원 𝐷가 커지면 가능도함수의 추정이 현실적으로 어려워진다.
따라서 나이즈베이즈 분류모형 (Naive Bayes classification model)에서는 모든 차원의 개별 독립변수가 서로 조건부독립 (conditional independent)이라는 가정을 사용한다. 이러한 가정을 나이브 가정 (naive assumption)이라고 한다.
나이브 가정으로 사용하면 벡터 𝑥의 결합확률분포함수는 개별 스칼라 원소 𝑥𝑑의 확률분포함수의 곱이 된다.
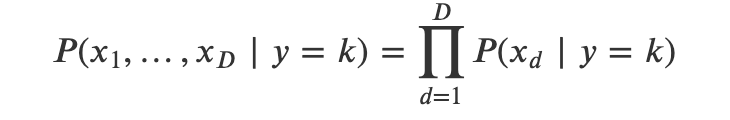
스칼라 원소 𝑥𝑑의 확률분포함수는 결합확률분포함수보다 추정하기 훨씬 쉽다.
가능도함수를 추정한 후에는 베이즈정리를 사용하여 조건부확률을 계산할 수 있다.
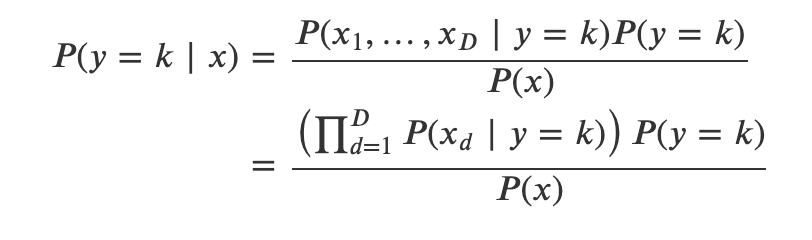
정규분포 가능도 모형
𝑥 벡터의 원소가 모두 실수이고 클래스마다 특정한 값 주변에서 발생한다고 하면 가능도 분포로 정규분포를 사용한다. 각 독립변수 𝑥𝑑마다, 그리고 클래스 𝑘마다 정규 분포의 기댓값 𝜇𝑑,𝑘 표준 편차가 달라진다. QDA 모형과는 달리 모든 독립변수들이 서로 조건부독립이라고 가정한다.
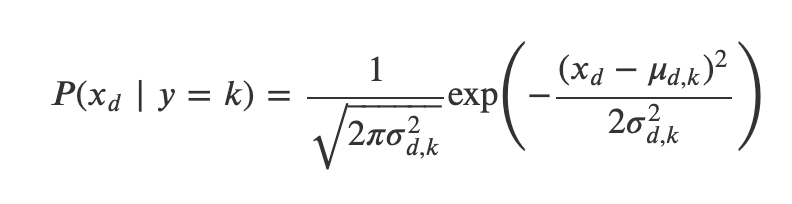
베르누이분포 가능도 모형
베르누이분포 가능도 모형에서는 각각의 𝑥=(𝑥1,…,𝑥𝐷)의 각 원소 𝑥𝑑가 0 또는 1이라는 값만을 가질 수 있다. 즉 독립변수는 𝐷개의 독립적인 베르누이 확률변수, 즉 동전으로 구성된 동전 세트로 표현할 수 있다. 이 동전들의 모수 𝜇𝑑는 동전 𝑑마다 다르다.
그런데 클래스 𝑦=𝑘 (𝑘=1,…,𝐾)마다도 𝑥𝑑가 1이 될 확률이 다르다. 즉, 동전의 모수 𝜇𝑑,𝑘는 동전 𝑑마다 다르고 클래스 𝑘마다도 다르다. 즉, 전체 𝐷×𝐾의 동전이 존재하며 같은 클래스에 속하는 𝐷개의 동전이 하나의 동전 세트를 구성하고 이러한 동전 세트가 𝐾개 있다고 생각할 수 있다.
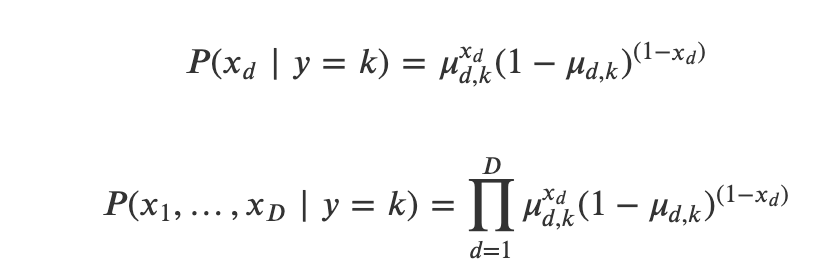
이러한 동전 세트마다 확률 특성이 다르므로 베르누이분포 가능도 모형을 기반으로 하는 나이브베이즈 모형은 동전 세트를 𝑁번 던진 결과로부터 1,…,𝐾 중 어느 동전 세트를 던졌는지를 찾아내는 모형이라고 할 수 있다.
다항분포 가능도 모형
다항분포 모형에서는 𝑥 벡터가 다항분포의 표본이라고 가정한다. 즉, 𝐷개의 면을 가지는 주사위를 던져서 나온 결과로 본다. 예를 들어 𝑥가 다음과 같다면,
$$ 𝑥=(1,4,0,5) $$
4면체 주사위를 10번 던져서 1인 면이 1번, 2인 면이 4번, 4인 면이 5번 나온 결과로 해석한다.
각 클래스마다 주사위가 다르다고 가정하므로 𝐾개의 클래스를 구분하는 문제에서는 𝐷개의 면을 가진 주사위가 𝐾개 있다고 본다.

따라서 다항분포 가능도 모형을 기반으로 하는 나이브베이즈 모형은 주사위를 던진 결과로부터 1,…,𝐾 중 어느 주사위를 던졌는지를 찾아내는 모형이라고 할 수 있다.
정규분포 나이브베이즈 모형
np.random.seed(0)
rv0 = sp.stats.multivariate_normal([-2, -2], [[1, 0.9], [0.9, 2]])
rv1 = sp.stats.multivariate_normal([2, 2], [[1.2, -0.8], [-0.8, 2]])
X0 = rv0.rvs(40)
X1 = rv1.rvs(60)
X = np.vstack([X0, X1])
y = np.hstack([np.zeros(40), np.ones(60)])
xx1 = np.linspace(-5, 5, 100)
xx2 = np.linspace(-5, 5, 100)
XX1, XX2 = np.meshgrid(xx1, xx2)
plt.grid(False)
plt.contour(XX1, XX2, rv0.pdf(np.dstack([XX1, XX2])), cmap=mpl.cm.cool)
plt.contour(XX1, XX2, rv1.pdf(np.dstack([XX1, XX2])), cmap=mpl.cm.hot)
plt.scatter(X0[:, 0], X0[:, 1], marker="o", c='b', label="y=0")
plt.scatter(X1[:, 0], X1[:, 1], marker="s", c='r', label="y=1")
plt.legend()
plt.title("데이터의 확률분포")
plt.axis("equal")
plt.show()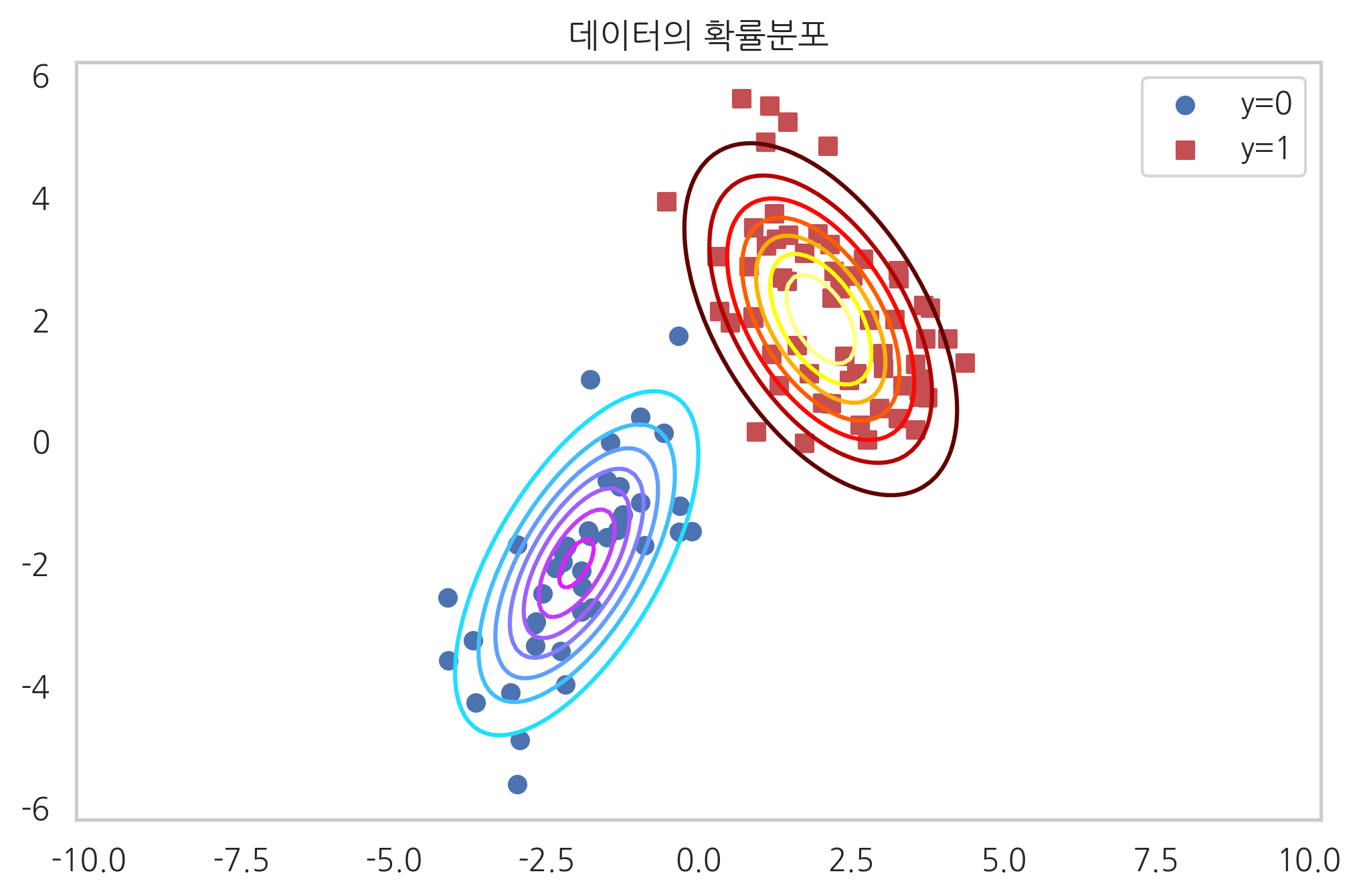
베르누이분포 나이브베이즈 모형
전자우편과 같은 문서 내에 특정한 단어가 포함되어 있는지의 여부는 베르누이 확률변수로 모형화할 수 있다. 이렇게 독립변수가 0 또는 1의 값을 가지면 베르누이 나이브베이즈 모형을 사용한다.
스무딩
표본 데이터의 수가 적은 경우에는 베르누이 모수가 0 또는 1이라는 극단적인 모수 추정값이 나올 수도 있다. 하지만 현실적으로는 실제 모수값이 이런 극단적인 값이 나올 가능성이 적다. 따라서 베르누이 모수가 0.5인 가장 일반적인 경우를 가정하여 0이 나오는 경우와 1이 나오는 경우, 두 개의 가상 표본 데이터를 추가한다. 그러면 0이나 1과 같은 극단적인 추정값이 0.5에 가까운 다음과 값으로 변한다. 이를 라플라스 스무딩 (Laplace smoothing) 또는 애드원 (Add-One) 스무딩이라고 한다.
7.2 나이브베이즈 분류모형 — 데이터 사이언스 스쿨
.ipynb .pdf to have style consistency -->
datascienceschool.net
'Learning-driven Methodology > ML (Machine Learning)' 카테고리의 다른 글
| 08. 텍스트 마이닝 (Text mining) (0) | 2021.12.15 |
|---|---|
| 07. SVM (Support Vector Machine) (0) | 2021.12.15 |
| 06. KNN (K-Nearest Neighbor) (0) | 2021.12.08 |
| 04. 군집 분석 (Clustering) (0) | 2021.12.08 |
| 03. 회귀분석 (Regression Analysis) (0) | 2021.12.08 |



