What is a Signal?
신호는 정보를 전달하고 시간, 공간 또는 기타 독립 변수 또는 변수에 따라 변하는 모든 물리량으로 정의된다. 과학 및 공학의 세계는 음성, 텔레비전, 원격 우주 탐사선의 이미지, 심장과 뇌에서 생성된 전압, 레이더 및 sonar echos, 지진 진동, GPS 위성의 신호, 인간 유전자의 신호 등 수많은 신호로 가득 차 있다.
What is a System?
시스템은 수학적으로 입력 신호 x(t)를 출력 신호 y(t)로 매핑하는 변환으로 정의된다. ℜ는 연산자이다.

예를 들어, 통신 시스템 자체는 송신기, 채널 및 수신기의 조합이다. 통신 시스템은 음성 신호를 입력으로 받아 원래 입력 신호의 추정치인 출력 신호로 변환한다.
Elementary Operations on Signals
많은 실제 상황에서 독립 변수 t의 수정과 관련된 신호를 고려해야 한다. 시간 이동, 시간 스케일링 및 시간 반전을 포함한 신호에 대한 설명이 필요하다.

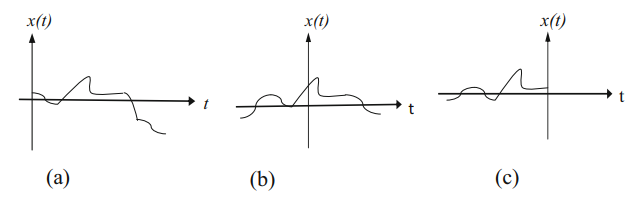
1. Time Shifting

신호 x(t)라 할 때, t0만큼 시간 이동된 경우 x(t)의 시간 이동된 버전은 x(t t0)로 표시된다. 두 신호 x(t) 및 x(t t0)은 모양이 동일하지만 서로에 대해 시간 이동된다. t0이 양수이면 신호 x(t)가 t0만큼 지연된다 (오른쪽으로 이동). t0이 음수이면 신호가 t0만큼 전진 (왼쪽으로 이동)된다. 이러한 방식과 관련된 신호는 수중 음파 탐지기, 지진 신호 처리, 레이더 및 GPS와 같은 응용 프로그램에서 발생한다. 그림 (a)에 나타난 신호 x(t)를 t0 = 2초만큼 쉬프트시키면 그림 (b)와 같이 x(t-2)가 된다. 즉, x(t)가 지연 (오른쪽 이동)된다. 2초로. 신호가 2초 전진(왼쪽 시프트)되면 그림 (c)와 같이 x(t+2)를 얻습니다. 즉, x(t)가 2초 전진 (왼쪽 이동)된다.
2. Time Scaling
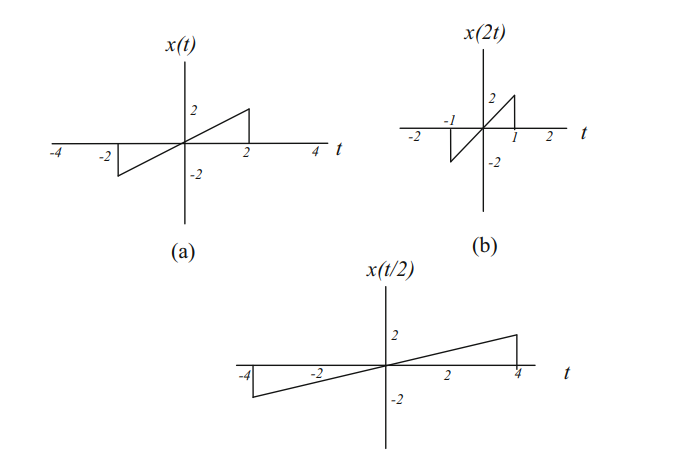
신호의 압축 또는 확장을 시간 스케일링이라고 한다. (a)의 신호 x(t)를 시간적으로 2배 압축하면 그림 (b)와 같이 x(2t)가 된다. 신호 x(t)를 2배로 확장하면 (c)와 같이 x(t/2)를 얻을 수 있다.
3. Time Reversal
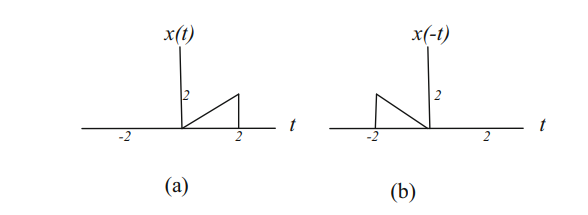
신호 x(-t)를 신호 x(t)의 시간 반전이라고 합니다. x(-t)는 t = 0에 대한 반사에 의해 신호 x(t)에서 얻는다. 신호 x(t)는 그림 (a)에 표시되고 시간 반전 신호 x(-t)는 (b)이다.
Classification of Signals
신호는 여러 가지 방법으로 분류할 수 있다. 신호의 몇 가지 중요한 분류는 다음과 같다.
1. Continuous-Time and Discrete-Time Signals

연속 시간 신호는 독립 변수 값의 연속에 대해 정의된다. 연속시간 신호의 경우 독립변수 t는 그림 (a)와 같이 연속적이다. 이산 시간 신호는 이산 시간에만 정의되며 이러한 신호에 대해 독립 변수 n은 그림 (b)와 같이 진폭 값의 이산 집합만 취한다.
2. Analog and Digital Signals
아날로그 신호는 진폭이 연속 범위에서 임의의 값을 가질 수 있는 연속 시간 신호이다. 디지털 신호는 이산 값 집합만 가질 수 있는 이산 시간 신호이다. 이산 시간 신호를 디지털 신호로 변환하는 과정을 양자화라고 한다.
3. Periodic and Aperiodic Signals
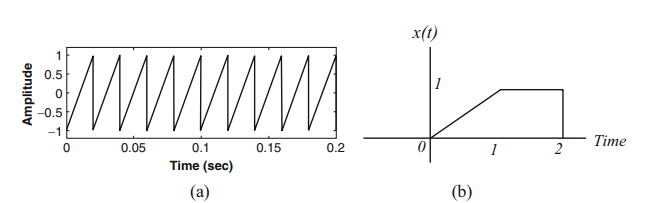
신호 x(t)는 t의 모든 값에 대해 주기성, 즉 x(t+T)=x(t)를 나타내는 경우 주기 T (0이 아닌 양의 값)로 주기적이라고 한다. 주기 신호는 T의 시간 이동에 의해 변하지 않는 성질을 가지고 있다. 위의 주기 성질을 만족하지 않는 신호를 비주기 신호라고 한다. 그림 (b)의 신호는 비주기적 신호의 한 예이다.
4. Even and Odd Signals

연속 시간 신호는 x(-t) = x(t)일 때 even이라고 한다. 연속시간 신호는 x(-t) = -x(t)일 때 odd라고 한다. odd 신호는 비대칭 신호라고도 한다. 짝수 및 홀수 신호의 예는 각각 그림 (a) 및 그림 (b)에 나와 있다.

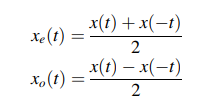
5. Causal, Noncausal, and Anticausal Signal
인과 신호는 음수 시간에 대해 0 값을 갖는 신호이다. 즉, t < 0이다. 음수 시간과 양수 시간 모두에 대해 0이 아닌 값이 있는 경우 신호는 비인과적이다. 반인과 신호는 양의 시간에 대해 0 값, 즉 t > 0을 갖는다. 인과 신호, 비인과 신호 및 반인과 신호의 예는 각각 그림 (a), (b) 및 (c)에 나와 있다.
6. Energy and Power Signals
유한 에너지를 가진 신호 x(t), 즉 진폭을 시간 0에서 무한으로 가는 것을 에너지 신호라고 하는 반면, 유한하고 0이 아닌 전력을 갖는 신호 x(t)는 전력 신호라고 한다. 신호 x(t)의 순시 전력 p(t)는 다음과 같이 표현할 수 있다.

7. Deterministic and Random Signals

주어진 시간 동안 결정적 신호의 값은 그림 (a)와 같이 완전히 지정된다. 따라서 결정론적 신호는 수학적으로 시간의 함수로 설명될 수 있다. 무작위 신호는 주어진 시간에 그림 (b)와 같이 통계적으로 특성화된 무작위 값을 취한다. 노이즈는 랜덤 신호의 일반적인 예이다.
'Signal Processing' 카테고리의 다른 글
| 02. Continuous-Time Signals and Systems (1) (0) | 2022.03.11 |
|---|---|
| 01. Introduction (MATLAB) (0) | 2022.03.11 |
| 01. Introduction (3) (0) | 2022.03.11 |
| 01. Introduction (2) (0) | 2022.03.11 |
| 신호 및 시스템 (Signals and Systems) (0) | 2022.03.10 |



