728x90
반응형
SMALL
영점 교차율 (Zero-crossing rate)
다양한 음성 및 오디오 파형을 보면 내용에 따라 부드러움 (smoothness)이 많이 다르다는 것을 알 수 있다. 예를 들어, 유성음은 무성음보다 더 부드럽다. 따라서, 부드러움은 신호의 유익한 특성이다.
신호의 부드러움을 측정하는 매우 간단한 방법은 해당 신호 세그먼트 내에서 제로 크로싱 수를 계산하는 것이다. 음성 신호는 천천히 진동한다. 예를 들어, 100Hz 신호는 초당 0을 100 교차하는 반면 무성 마찰음은 초당 3000을 교차할 수 있다. 창에서 신호에 대한 제로 크로싱 구현은 다음과 같다.
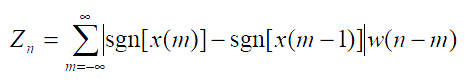
# static example of zero-crossing
from ipywidgets import *
import IPython.display as ipd
from ipywidgets import interactive
import numpy as np
import scipy
from scipy.io import wavfile
from scipy import signal
import matplotlib.pyplot as plt
%matplotlib inline
filename = 'sample.wav'
fs, data = wavfile.read(filename)
data = data.astype(np.int16)
data = data[:, 0]
data_length = int(len(data))
window_length_ms = 10
window_length = int(window_length_ms*fs/1000.)
t = np.arange(0,data_length)/fs
# Hann window
window_function = np.sin(np.pi*np.arange(.5/window_length,1,1/window_length))**2
window_position = int(2.2*fs)
if window_position > data_length-window_length:
window_position = data_length-window_length
ix = window_position + np.arange(0,window_length,1)
zcr = np.sum(np.abs(np.diff(np.sign(data[ix]),axis=0)),axis=0)//2
zcr_vec = np.abs(np.diff(np.sign(data[ix]),axis=0))
zcr_idx = np.where(zcr_vec > 0)
fig = plt.figure(figsize=(10, 4))
plt.plot(t[ix],data[ix])
plt.plot(t[ix[zcr_idx]],0*data[ix[zcr_idx]],'rx')
plt.title('Window of signal with ' +str(zcr) + ' zero-crossings')
plt.xlabel('Time (s)')
plt.ylabel('Amplitude')
plt.tight_layout()
plt.show()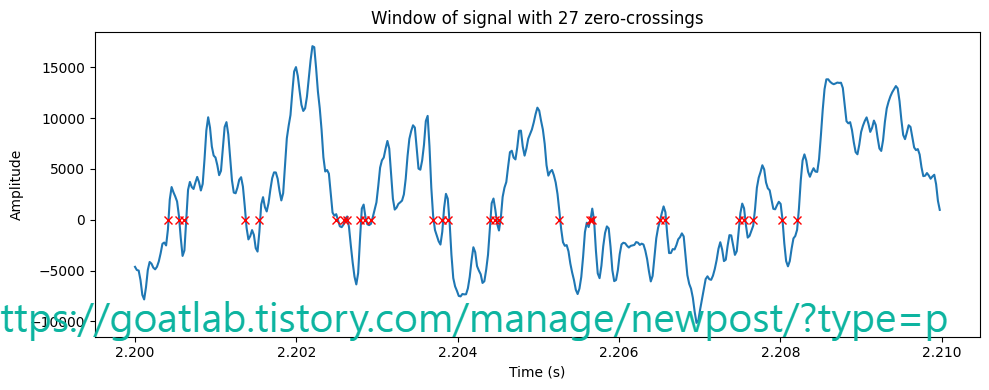
# static example of zero-crossing
from ipywidgets import *
import IPython.display as ipd
from ipywidgets import interactive
import numpy as np
import scipy
from scipy.io import wavfile
from scipy import signal
import matplotlib.pyplot as plt
%matplotlib inline
filename = 'sample.wav'
fs, data = wavfile.read(filename)
data = data.astype(np.int16)
data = data[:, 0]
data_length = int(len(data))
window_length_ms = 10
window_length = int(window_length_ms*fs/1000.)
t = np.arange(0,data_length)/fs
# Hann window
window_function = np.sin(np.pi*np.arange(.5/window_length,1,1/window_length))**2
window_position = int(2.2*fs)
if window_position > data_length-window_length:
window_position = data_length-window_length
ix = window_position + np.arange(0,window_length,1)
zcr = np.sum(np.abs(np.diff(np.sign(data[ix]),axis=0)),axis=0)//2
zcr_vec = np.abs(np.diff(np.sign(data[ix]),axis=0))
zcr_idx = np.where(zcr_vec > 0)
fig = plt.figure(figsize=(10, 4))
plt.plot(t[ix],data[ix])
plt.plot(t[ix[zcr_idx]],0*data[ix[zcr_idx]],'rx')
plt.title('Window of signal with ' +str(zcr) + ' zero-crossings')
plt.xlabel('Time (s)')
plt.ylabel('Amplitude')
plt.tight_layout()
plt.show()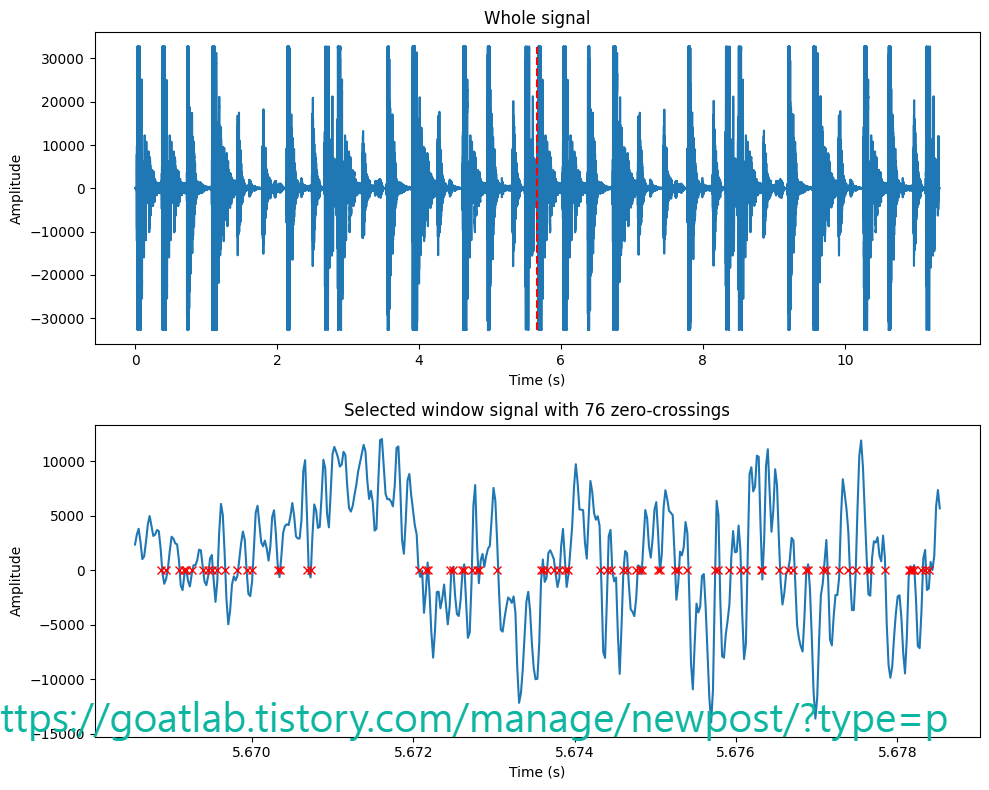
신호의 영교차율을 계산하려면 각 연속 샘플 쌍의 부호를 비교해야 한다. 즉, 길이가 N인 신호의 경우 O(N) 연산이 필요다. 이러한 계산은 구현하기도 매우 간단하므로 제로 크로싱 속도는 복잡성이 낮은 어플리케이션에 대한 매력적인 척도가 된다. 그러나 영교차율에는 다음과 같은 많은 단점도 있다.
|
영교차율의 대안은 (lag-1)에서 자기 상관을 계산하는 것이다. 짧은 세그먼트에서도 추정할 수 있으며 연속 값이며 산술 복잡도 (arithmetic complexity)도 O(N)다.
import numpy as np
import matplotlib.pyplot as plt
from scipy.io import wavfile
# read from storage
filename = 'sample.wav'
fs, data = wavfile.read(filename)
data = np.float64(data)
# window parameters in milliseconds
window_length_ms = 30
window_step_ms = 5
window_step = int(np.round(fs*window_step_ms/1000))
window_length = window_step*2
window_count = int(np.floor((data.shape[0]-window_length)/window_step)+1)
# Extract windows
window_matrix = np.zeros([window_length,window_count],dtype=np.float64)
for window_ix in range(window_count):
window_matrix[:,window_ix] = data[window_ix*window_step+np.arange(window_length), 0]
# Count zero crossings in each window
zcr = np.sum(np.abs(np.diff(np.sign(window_matrix),axis=0)),axis=0)
# Correlation lag-1
xcorr1 = np.mean(window_matrix[0:-2,:]*window_matrix[1:-1,:],axis=0)/np.mean(window_matrix**2,axis=0)
plt.figure(figsize=[10,8])
t = np.linspace(0,len(data)/fs,len(data))
plt.subplot(311)
plt.plot(t,data/np.max(np.abs(data)))
plt.ylabel('Amplitude')
plt.title('Original waveform')
t = np.linspace(0,len(data)/fs,window_count)
plt.subplot(312)
plt.plot(t,zcr)
plt.ylabel('Zero-crossing rate')
plt.title('Zero-crossing rate')
plt.subplot(313)
plt.plot(t,xcorr1)
plt.xlabel('Time (s)')
plt.ylabel('Lag-1 autocorrelation')
plt.title('Lag-1 autocorrelation')
plt.tight_layout()
plt.show()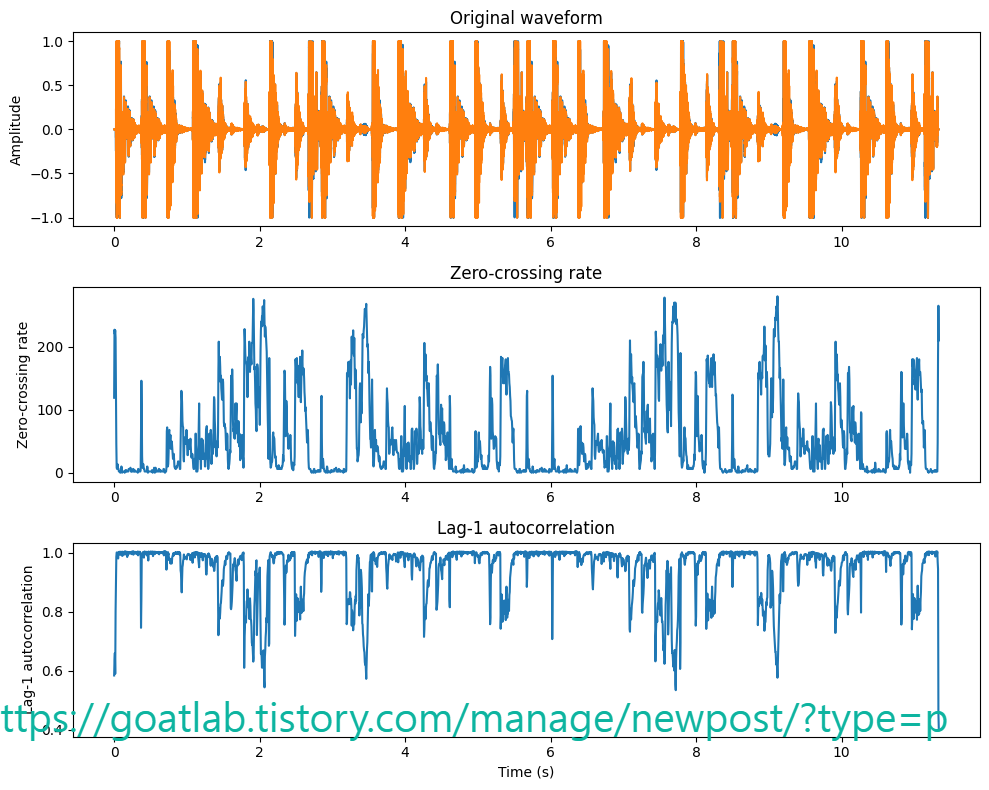
728x90
반응형
LIST
'Linguistic Intelligence > Audio Processing' 카테고리의 다른 글
| 자기 상관 관계 및 공분산 (0) | 2024.04.24 |
|---|---|
| 음성 신호에서 스펙트로그램 해석 (0) | 2024.04.24 |
| 단시간 푸리에 변환 (STFT) (0) | 2024.04.23 |
| Sound Energy (0) | 2024.04.23 |
| 윈도우 기법 (Windowing) (0) | 2024.04.17 |



