단시간 푸리에 변환 (Short-Time Fourier Transform)
피치 (Pitch)는 높거나 낮은 음조가 무엇을 의미하는지 음조의 주파수에 대한 사람의 인식을 나타낸다. 신호의 푸리에 스펙트럼은 이러한 주파수 내용을 나타낸다. 이는 신호를 시각적으로 검사할 수 있기 때문에 스펙트럼을 작업하기에 직관적인 영역으로 만든다. 실제로, 이산 시간 신호를 사용하여 해당 시간-주파수 변환이 이산 푸리에 변환이 되도록 작업한다. 이는 길이 신호 X를 다음과 같이 N 계수의 복소수 값 주파수 영역 표현으로 매핑한다.
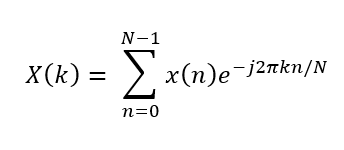
실수 값 입력의 경우 양수 및 음수 주파수 구성 요소는 서로의 복소 공액 (complex conjugates)이므로 고유한 정보 단위를 유지한다. 그러나 스펙트럼은 복소수 벡터이므로 시각화하기가 어렵다. 첫 번째 해결책은 크기 스펙트럼 또는 전력 스펙트럼을 플롯하는 것이다. 다양한 주파수 범위의 큰 차이로 인해 불행하게도 이러한 표현은 관련 정보를 쉽게 표시하지 않는다.
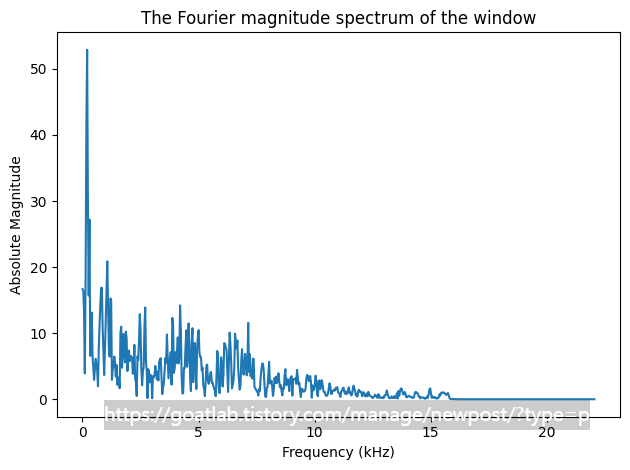
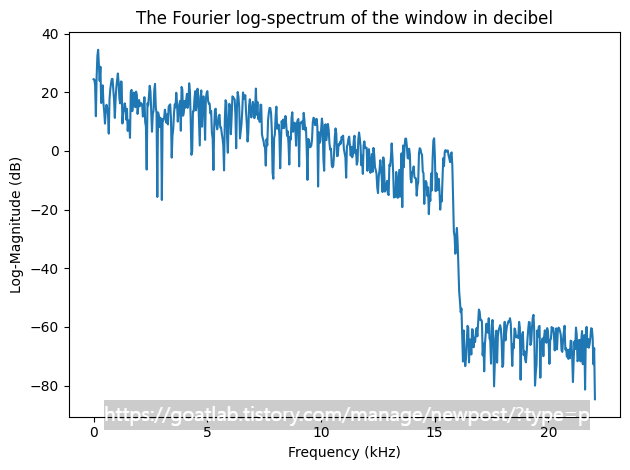
로그 스펙트럼은 스펙트럼의 가장 일반적인 시각화이며 데시벨 단위로 스펙트럼을 제공한다. 소리를 쉽게 해석할 수 있는 시각화를 제공하므로 유용하다.
import numpy as np
import matplotlib.pyplot as plt
from scipy.io import wavfile
import scipy
import scipy.fft
# read from storage
filename = 'sample.wav'
fs, data = wavfile.read(filename)
window_length_ms = 30
window_length = int(np.round(fs*window_length_ms/1000))
n = np.linspace(0.5,window_length-0.5,num=window_length)
# windowing function
windowing_fn = np.sin(np.pi*n/window_length)**2 # sine-window
windowpos = np.random.randint(int((len(data)-window_length)))
datawin = data[windowpos:(windowpos+window_length), 0]
datawin = datawin/np.max(np.abs(datawin)) # normalize
spectrum = scipy.fft.rfft(datawin*windowing_fn)
f = np.linspace(0.,fs/2,num=len(spectrum))
plt.plot(n*1000/fs,datawin)
plt.xlabel('Time (ms)')
plt.ylabel('Amplitude')
plt.title('A window of a signal without a windowing function (i.e. rectangular window)')
plt.axis([-10.,45.,-1.,1.])
plt.tight_layout()
plt.show()
#nx = np.concatenate(([-1000,0.],n,[window_length,window_length+1000]))
#datax = np.concatenate(([0.,0.],datawin,[0.,0.]))
#plt.plot(nx*1000/fs,datax)
#plt.xlabel('Time (ms)')
#plt.ylabel('Amplitude')
#plt.title('Signal with a rectangular window looks as if it had a discontinuity at the borders')
#plt.axis([-10.,45.,-1.,1.])
#plt.tight_layout()
#plt.show()
nx = np.concatenate(([-1000,0.],n,[window_length,window_length+1000]))
datax = np.concatenate(([0.,0.],datawin*windowing_fn,[0.,0.]))
plt.plot(nx*1000/fs,datax,label='Windowed signal')
plt.plot(n*1000/fs,windowing_fn,'--',label='Window function')
plt.legend()
plt.xlabel('Time (ms)')
plt.ylabel('Amplitude')
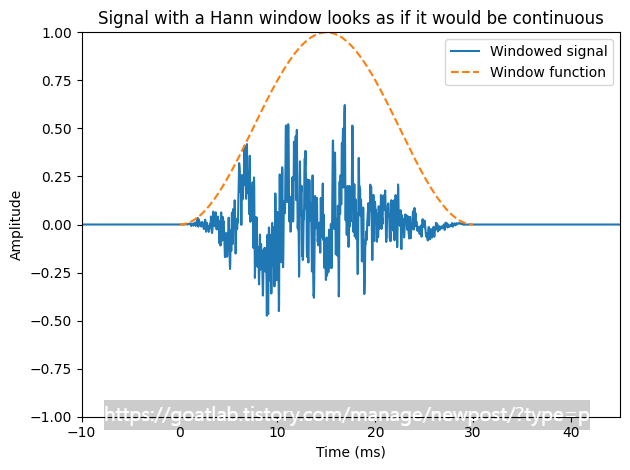
plt.title('Signal with a Hann window looks as if it would be continuous')
plt.axis([-10.,45.,-1.,1.])
plt.tight_layout()
plt.show()
plt.plot(f/1000,np.abs(spectrum))
plt.xlabel('Frequency (kHz)')
plt.ylabel('Absolute Magnitude')
plt.title('The Fourier magnitude spectrum of the window')
plt.tight_layout()
plt.show()
plt.plot(f/1000,20.*np.log10(np.abs(spectrum)))
plt.xlabel('Frequency (kHz)')
plt.ylabel('Log-Magnitude (dB)')
plt.title('The Fourier log-spectrum of the window in decibel')
plt.tight_layout()
plt.show()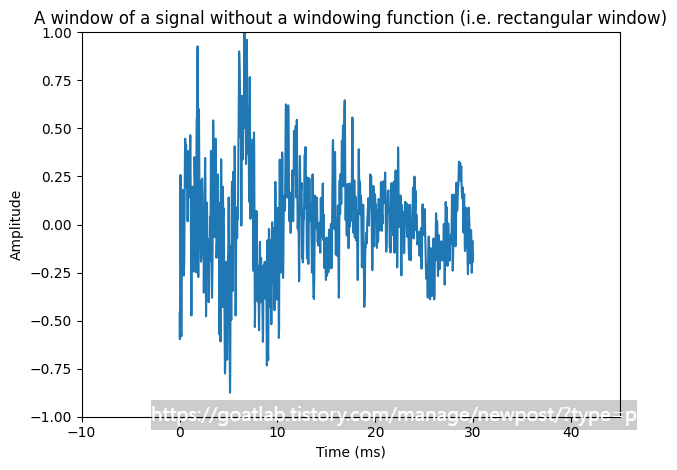
# interactive example of spectrum
from ipywidgets import *
import IPython.display as ipd
from ipywidgets import interactive
import numpy as np
import scipy
from scipy.io import wavfile
from scipy import signal
import matplotlib.pyplot as plt
%matplotlib inline
filename = 'sample.wav'
fs, data = wavfile.read(filename)
data = data.astype(np.int16)
data = data[:]
data_length = int(len(data))
def update(position_s=0.5*data_length/fs,window_length_ms=32.0):
ipd.clear_output(wait=True)
window_length = int(window_length_ms*fs/1000.)
t = np.arange(0,data_length)/fs
# Hann window
window_function = np.sin(np.pi*np.arange(.5/window_length,1,1/window_length))**2
window_position = int(position_s*fs)
if window_position > data_length-window_length:
window_position = data_length-window_length
ix = window_position + np.arange(0,window_length,1)
window = data[ix, 0]*window_function
X = scipy.fft.rfft(window.T,n=2*window_length)
dft_length = len(X)
f = np.arange(0,dft_length)*(fs/2000)/(dft_length)
fig = plt.figure(figsize=(10, 8))
#ax = fig.subplots(nrows=1,ncols=1)
plt.subplot(311)
plt.plot(t,data)
plt.plot([position_s, position_s],[np.min(data), np.max(data)],'r--')
plt.title('Whole signal')
plt.xlabel('Time (s)')
plt.ylabel('Amplitude')
plt.subplot(312)
plt.plot(t[ix],data[ix])
plt.title('Selected window signal at postion (s)')
plt.xlabel('Time (s)')
plt.ylabel('Amplitude')
plt.subplot(313)
plt.plot(f,20.*np.log10(np.abs(X)))
plt.title('Spectrum of window')
plt.xlabel('Frequency (kHz)')
plt.ylabel('Magnitude (dB)')
plt.tight_layout()
plt.show()
fig.canvas.draw()
interactive_plot = interactive(update,
#positions_s=widgets.FloatSlider(min=0., max=(data_length-window_length)/fs, value=1., step=0.01,layout=Layout(width='1500px')),
position_s=(0., data_length/fs,0.001),
window_length_ms=(2.0, 300.0, 0.5))
output = interactive_plot.children[-1]
output.layout.height = '600px'
style = {'description_width':'120px'}
interactive_plot.children[0].layout = Layout(width='760px')
interactive_plot.children[1].layout = Layout(width='760px')
interactive_plot.children[0].style=style
interactive_plot.children[1].style=style
interactive_plot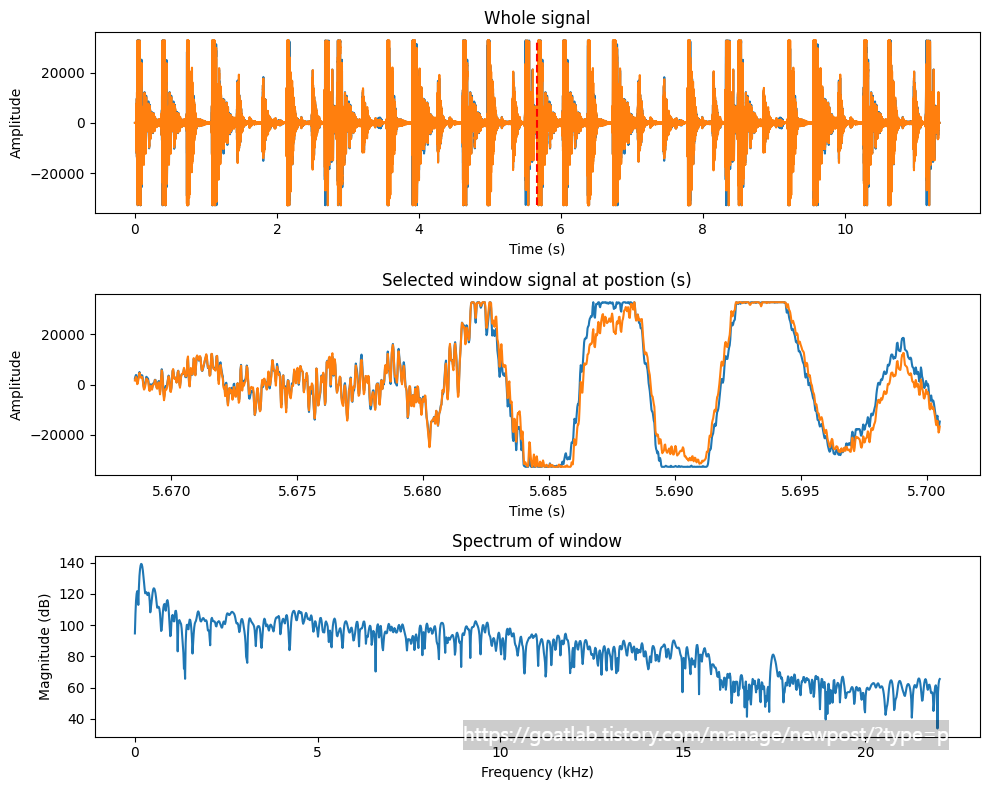
그러나 음성 신호는 비정상 신호이다. 음성 문장을 주파수 영역으로 변환하면 문장에 있는 모든 음소의 평균인 스펙트럼을 얻을 수 있지만, 종종 각 개별 음소 (phoneme)의 스펙트럼을 별도로 볼 수 있다. 이때, 신호를 더 짧은 세그먼트로 분할함으로써 특정 시점의 신호 속성에 집중할 수 있다.
각 윈도우의 이산 푸리에 변환 (DFT)을 윈도우화하고 취함으로써 신호의 단시간 푸리에 변환 (STFT)을 얻는다. 특히, 입력 신호와 window에 대해 변환은 다음과 같이 정의된다.
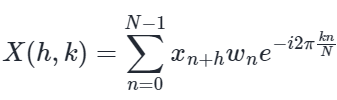
STFT는 음성 분석 및 처리에 가장 자주 사용되는 도구 중 하나이다. 시간에 따른 주파수 성분의 변화를 설명한다. 스펙트럼 자체와 마찬가지로 STFT의 장점 중 하나는 해당 매개변수가 물리적이고 직관적으로 해석된다는 것이다. 스펙트럼과 또 다른 평행점은 STFT의 출력이 복소수 값이라는 것이다. 그러나 스펙트럼이 벡터인 경우 STFT 출력은 행렬이다. 결과적으로 복소수 값 출력을 직접 시각화할 수 없다. 대신, STFT는 일반적으로 로그 스펙트럼을 사용하여 시각화된다. 그런 다음 이러한 2차원 로그 스펙트럼은 스펙트로그램으로 알려진 히트맵으로 시각화할 수 있다.
import numpy as np
from scipy.io import wavfile
import IPython.display as ipd
from scipy import signal
# read from storage
filename = 'sample.wav'
fs, data = wavfile.read(filename)
# resample to 16kHz for better visualization
target_fs = 16000
data = scipy.signal.resample(data, len(data)*target_fs//fs)
fs = target_fs
# ipd.display(ipd.Audio(data,rate=fs))
# window parameters in milliseconds
window_length_ms = 30
window_step_ms = 5
window_step = int(np.round(fs*window_step_ms/1000))
window_length = int(np.round(fs*window_length_ms/1000))
window_count = int(np.floor((data.shape[0]-window_length)/window_step)+1)
# windowing function
windowing_fn = np.sin(np.pi*np.linspace(0.5,window_length-0.5,num=window_length)/window_length)**2 # Hann-window
spectrogram_matrix = np.zeros([window_length,window_count],dtype=complex)
for window_ix in range(window_count):
data_window = np.multiply(windowing_fn,data[window_ix*window_step+np.arange(window_length), 0])
spectrogram_matrix[:,window_ix] = np.fft.fft(data_window)
fft_length = int((window_length+1)/2)
t = np.arange(0.,len(data),1.)/fs
plt.figure(figsize=(12,8))
plt.subplot(311)
plt.plot(t,data)
plt.xlabel('Time (s)')
plt.ylabel('Amplitude')
plt.title('Speech waveform')
plt.subplot(312)
plt.imshow(20*np.log10(0.2+np.abs(spectrogram_matrix[range(fft_length),:])),origin='lower',aspect='auto',extent=[0.,len(data)/fs,0.,fs/2000])
#plt.xticks(np.arange(0.,len(data)/fs,0.5));
plt.xlabel('Time (s)')
#plt.yticks(np.arange(0,fft_length,fft_length*10000/fs));
plt.ylabel('Frequency (10kHz)');
plt.title('Speech spectrogram')
plt.subplot(313)
plt.imshow(20*np.log10(0.2+np.abs(spectrogram_matrix[range(fft_length//2),:])),origin='lower',aspect='auto',extent=[0.,.5*len(data)/fs,0.,fs/2000])
plt.xlabel('Time (s)')
#plt.yticks(np.arange(0,fft_length,fft_length*10000/fs));
plt.ylabel('Frequency (10kHz)');
plt.title('Speech spectrogram zoomed in to lower frequencies')
plt.tight_layout()
plt.show()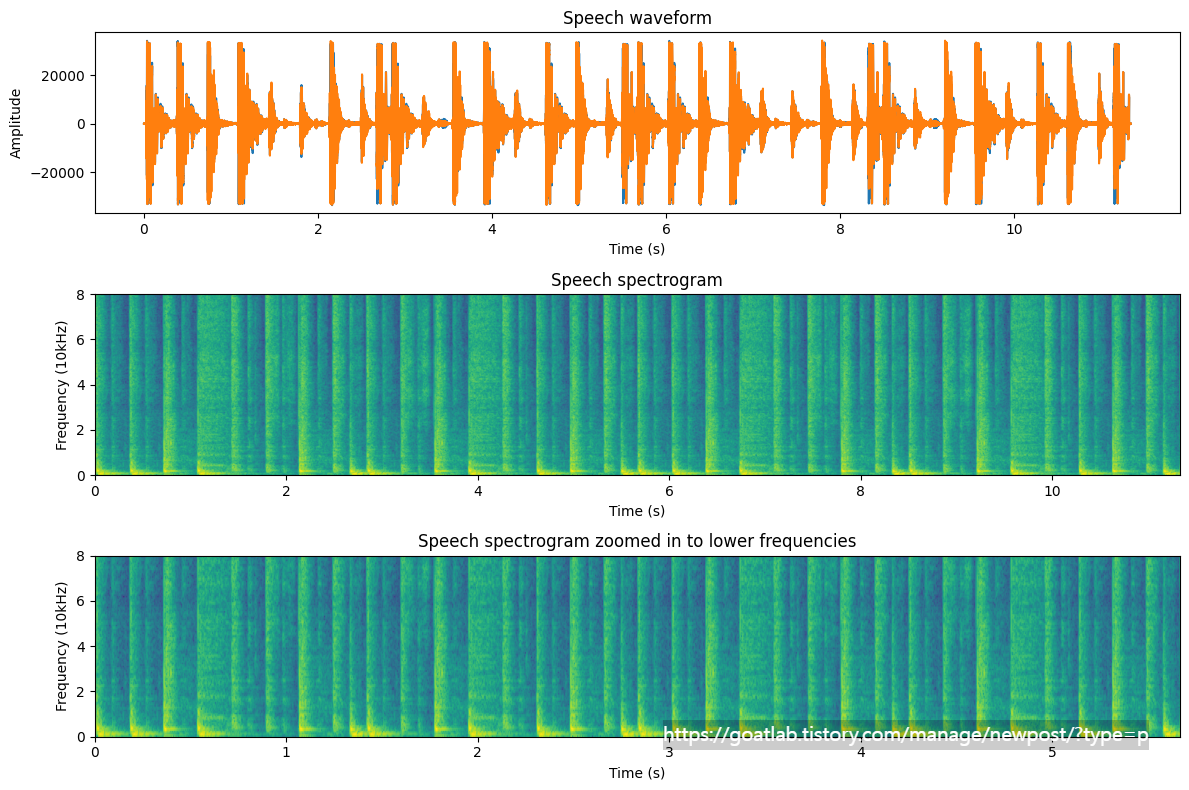
스펙트로그램에서 음성을 보면 신호의 많은 중요한 특징을 명확하게 관찰할 수 있다.
|
from ipywidgets import *
import IPython.display as ipd
from ipywidgets import interactive
import numpy as np
import scipy
from scipy.io import wavfile
from scipy import signal
import matplotlib.pyplot as plt
%matplotlib inline
filename = 'sample.wav'
fs, data = wavfile.read(filename)
data = data.astype(np.int16)
data = data[:, 0]
data_length = int(len(data))
def update(window_length_ms=32.0, window_step_ms=16.0):
ipd.clear_output(wait=True)
window_length = int(window_length_ms*fs/1000.)
window_step = int(window_step_ms*fs/1000.)
window_count = (data_length - window_length)//window_step + 1
dft_length = (window_length + 1)//2
# sine window
window_function = np.sin(np.pi*np.arange(.5/window_length,1,1/window_length))**2
windows = np.zeros([window_length, window_count])
for k in range(window_count):
ix = k*window_step + np.arange(0,window_length,1)
windows[:,k] = data[ix]*window_function
X = scipy.fft.rfft(windows.T,n=2*window_length)
fig = plt.figure(figsize=(12, 4))
ax = fig.subplots(nrows=1,ncols=1)
ax.imshow(20.*np.log10(np.abs(X.T)),origin='lower')
plt.axis('auto')
plt.show()
fig.canvas.draw()
interactive_plot = interactive(update, window_length_ms=(2.0, 300.0, 0.5), window_step_ms=(1.,50.,0.01))
output = interactive_plot.children[-1]
output.layout.height = '350px'
interactive_plot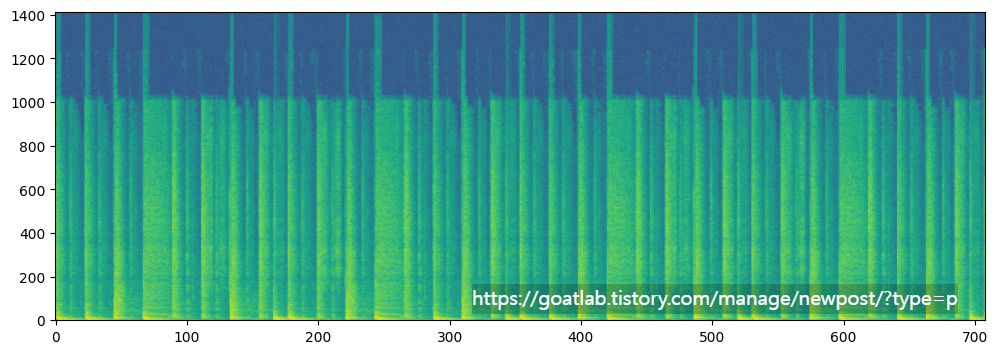
'Linguistic Intelligence > Audio Processing' 카테고리의 다른 글
| 자기 상관 관계 및 공분산 (0) | 2024.04.24 |
|---|---|
| 음성 신호에서 스펙트로그램 해석 (0) | 2024.04.24 |
| Sound Energy (0) | 2024.04.23 |
| 윈도우 기법 (Windowing) (0) | 2024.04.17 |
| 파형 (Waveform) (0) | 2024.03.27 |



