Welch's Method
Peter D. Welch의 이름을 딴 Welch의 방법은 스펙트럼 밀도 추정 (spectral density estimation)을 위한 접근 방식이다. 이는 다양한 주파수에서 신호의 전력을 추정하기 위해 물리학, 공학 및 응용 수학에 사용된다. 이 방법은 신호를 시간 영역에서 주파수 영역으로 변환한 결과인 주기도 (periodogram) 스펙트럼 추정값을 사용하는 개념을 기반으로 한다. Welch의 방법은 표준 주기도 스펙트럼 추정 방법과 Bartlett의 방법을 개선한 것이다. 이는 주파수 분해능을 줄이는 대가로 추정된 전력 스펙트럼 의 잡음을 줄인다는 점이다. 불완전하고 유한한 데이터로 인해 발생하는 잡음으로 인해 Welch 방법의 잡음 감소가 필요한 경우가 많다.
전력 스펙트럼을 추정하기 위한 Welch의 방법 (주기도 방법이라고도 함) 은 시간 신호를 연속적인 블록으로 나누고 각 블록에 대한 주기도를 형성한 후 평균을 구하는 방식으로 수행된다. x 신호에서 제로 패딩된 m번째 window 프레임을 다음과 같이 나타낸다.
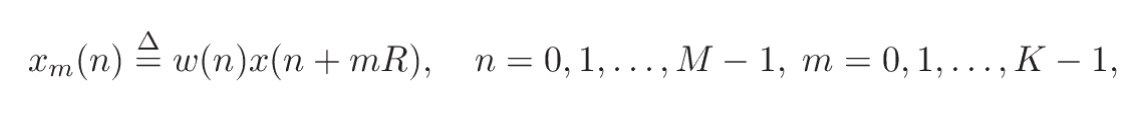
여기서는 R은 window hop 크기로 정의된다. K는 사용 가능한 프레임 수를 나타낸다. 그러면 m번째 블록의 주기도는 m번째와 같이 지정된다.
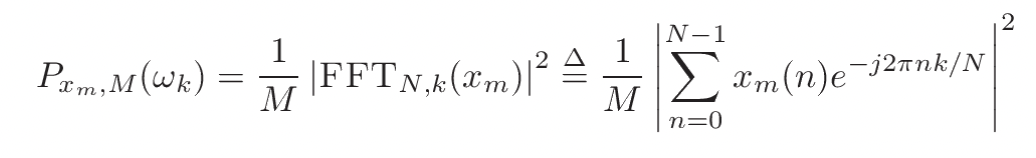
전력 스펙트럼 밀도에 대한 Welch 추정값은 다음과 같이 지정된다.
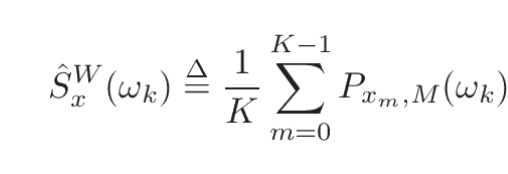
즉, 단지 전체 시간에 걸친 주기도의 평균일 뿐이다. w(n)이 직사각형 window일 때, 주기도는 겹치지 않는 연속적인 데이터 블록들로부터 형성된다. 다른 window 유형들의 경우 일반적으로 겹친다.
scipy.signal.welch
10kHz에서 샘플링된 0.001V**2/Hz의 백색 잡음으로 손상된 1234Hz에서 2Vrms sine 파형 테스트 신호를 생성한다.
import numpy as np
from scipy import signal
import matplotlib.pyplot as plt
rng = np.random.default_rng()
fs = 10e3
N = 1e5
amp = 2*np.sqrt(2)
freq = 1234.0
noise_power = 0.001 * fs / 2
time = np.arange(N) / fs
x = amp*np.sin(2*np.pi*freq*time)
x += rng.normal(scale=np.sqrt(noise_power), size=time.shape)
f, Pxx_den = signal.welch(x, fs, nperseg=1024)
plt.semilogy(f, Pxx_den)
plt.ylim([0.5e-3, 1])
plt.xlabel('frequency [Hz]')
plt.ylabel('PSD [V**2/Hz]')
plt.show()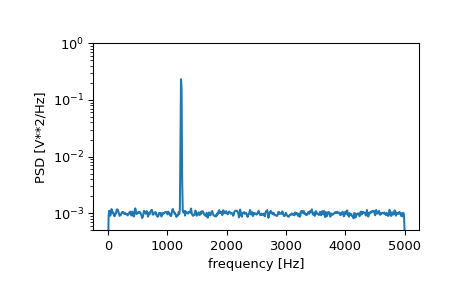
f, Pxx_spec = signal.welch(x, fs, 'flattop', 1024, scaling='spectrum')
plt.figure()
plt.semilogy(f, np.sqrt(Pxx_spec))
plt.xlabel('frequency [Hz]')
plt.ylabel('Linear spectrum [V RMS]')
plt.show()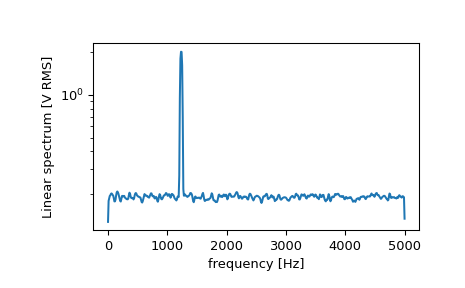
신호의 작은 부분의 진폭을 50만큼 증가시킴으로써 신호에 불연속성을 도입하면 평균 전력 스펙트럼 밀도의 손상을 볼 수 있지만 중위수 평균을 사용하는 것이 정상적인 행동을 더 잘 추정한다.
x[int(N//2):int(N//2)+10] *= 50.
f, Pxx_den = signal.welch(x, fs, nperseg=1024)
f_med, Pxx_den_med = signal.welch(x, fs, nperseg=1024, average='median')
plt.semilogy(f, Pxx_den, label='mean')
plt.semilogy(f_med, Pxx_den_med, label='median')
plt.ylim([0.5e-3, 1])
plt.xlabel('frequency [Hz]')
plt.ylabel('PSD [V**2/Hz]')
plt.legend()
plt.show()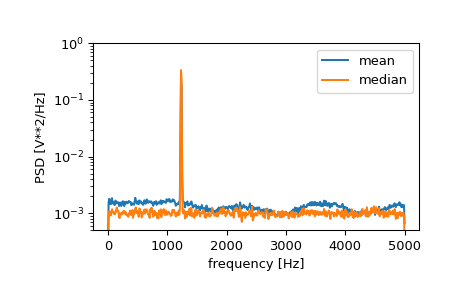
주기도는 광의의 정상 과정의 실제 파워 스펙트럼 밀도에 대한 일치 추정량 (consistent estimator)이 아니다. 주기도의 분산을 줄이기 위한 Welch 기법은 시계열을 세그먼트로 나누는데 이 세그먼트는 보통 중첩된다. Welch 방법은 각 세그먼트에 대해 수정된 주기도를 계산한 후 이러한 추정값의 평균을 내어 파워 스펙트럼 밀도의 추정값을 생성한다. 이 과정이 광의의 정상 과정이고 Welch 방법이 시계열의 각기 다른 세그먼트에 대한 PSD 추정값을 사용하기 때문에 수정된 주기도는 실제 PSD의 대략적으로 상관 관계가 없는 추정값을 나타내며 평균화를 통해 변동성이 줄어든다. Welch 방법이 수정된 주기도의 평균에 이르도록 일반적으로 세그먼트에 해밍 윈도우와 같은 윈도우 함수를 곱한다. 세그먼트은 일반적으로 중첩되므로 한 세그먼트에서 윈도우에 인해 가늘어진 세그먼트의 시작과 끝에 있는 데이터 값은 인접한 세그먼트의 끝부분에서 떨어진 위치에 나타난다. 이는 윈도우 생성으로 인해 정보가 손실되는 것을 방지한다.
https://ccrma.stanford.edu/~jos/sasp/Welch_s_Method.html
Welch's Method
ccrma.stanford.edu
'Signal Processing' 카테고리의 다른 글
| 코덱 (Codec) (0) | 2023.10.25 |
|---|---|
| Mel Spectrogram (0) | 2023.09.13 |
| [Signal Processing] 이동 평균 필터 (Moving average filter) (0) | 2023.07.06 |
| Wavelet 변환 (0) | 2022.04.19 |
| Use of AR Models to Estimate Spectra (0) | 2022.04.13 |



