728x90
반응형
SMALL
주성분 분석 (Principal Component Analysis, PCA)
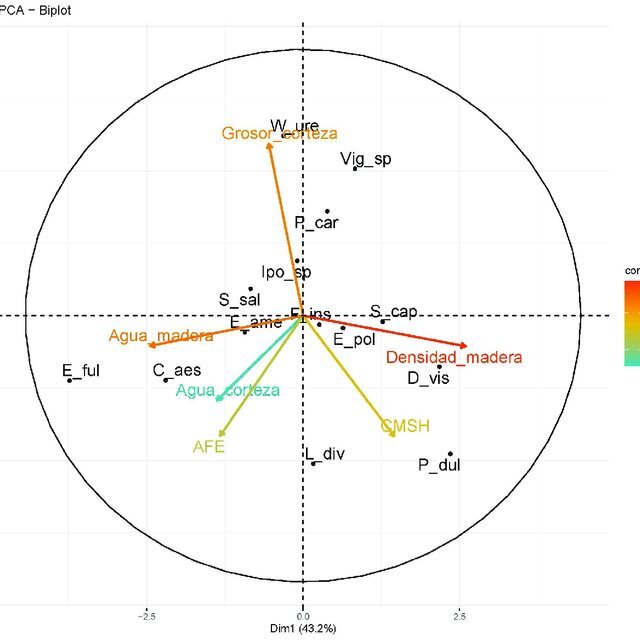
주성분 분석 (Principal Component Analysis, PCA)은 가장 널리 사용되는 차원 축소 기법 중 하나로, 원 데이터의 분포를 최대한 보존하면서 고차원 공간의 데이터들을 저차원 공간으로 변환한다.
데이터 집합을 새로운 좌표축으로 변환시키는 방법이다. 수 많은 정보의 홍수에서 이를 활용하기 위해 정보 손실을 최소화하면서 차수를 낮출 때 사용하는 방법이다. 정보를 각각 서로 간에 독립인 좌표축 들로 재구성하여, 최소한의 차원으로 최대한의 설명력을 높인다.
n_components
from sklearn.decomposition import PCA
# PCA 모델을 생성
pca = PCA()
# PCA 모델을 데이터에 fitting
pca.fit(data)
# 누적 설명 분산을 기반으로 주성분의 수를 선택
explained_variance = pca.explained_variance_ratio_
cumulative_explained_variance = np.cumsum(explained_variance)
# 원하는 누적 설명 분산 비율을 설정
desired_variance = 0.95
# 누적 설명 분산이 원하는 비율에 도달할 때까지 주성분의 수를 결정
n_components = np.argmax(cumulative_explained_variance >= desired_variance) + 1
# 선택된 주성분의 수를 출력
print("선택된 주성분의 수:", n_components)
표준화
먼저, PCA를 적용하기 전에 데이터를 표준화한다. 이후, PCA를 적용하여 주성분의 개수에 따른 설명 가능한 분산의 비율을 계산한다. 설명 가능한 분산의 비율이 90% 이상이 되는 주성분의 개수를 선택한다.
from sklearn.decomposition import PCA
from sklearn.preprocessing import StandardScaler
X, y = load_dataset()
X_std = StandardScaler().fit_transform(X)
pca = PCA()
pca.fit(X_std)
cumulative_variance_ratio = np.cumsum(pca.explained_variance_ratio_)
n_components = np.argmax(cumulative_variance_ratio >= 0.9) + 1728x90
반응형
LIST
'Data-driven Methodology > DS (Data Science)' 카테고리의 다른 글
| [Data Science] 불균형한 데이터 균형 조정 (0) | 2023.12.08 |
|---|---|
| [Data Science] Random UnderSampling (0) | 2023.10.04 |
| [Data Science] 데이터 불균형 (0) | 2023.09.06 |
| [Data Science] 탐색적 데이터 분석 (Exploratory Data Analysis) (0) | 2023.07.17 |
| [Data Science] 모델 평가 (0) | 2022.11.29 |



