Adaptive Exponential Integrate and Fire model (AdEx)

good neuron model이 되기 위한 조건
- Can predict spike times
- Can predict subthreshold voltage
- Can interpret easily (not a ‘black box’)
- Can account flexibly for a variety of phenomena
- Can optimize parameters for systematic procedure
1-dimensional (nonlinear) integrate and fire 모델에서는 다양한 dynamics를 표현할 수 없다.
따라서, best choice 𝑓 : linear + exponential
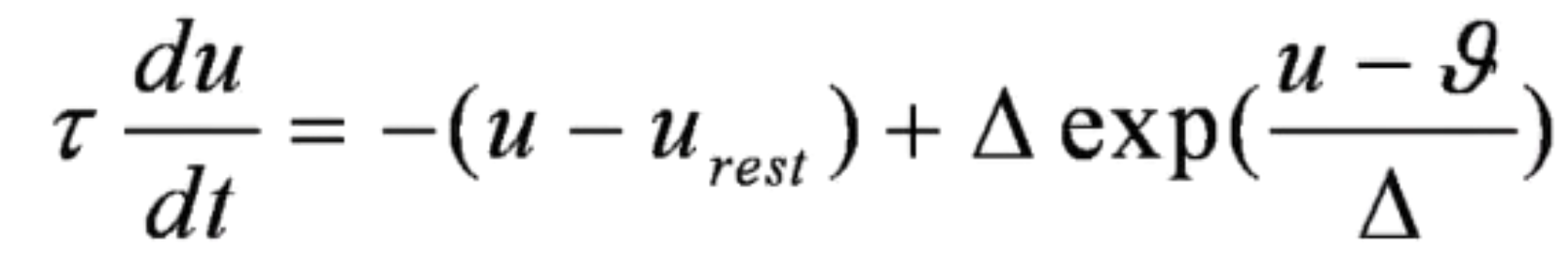
Δ : the slope factor ; typically chosen in the range between 0 and 5ms
𝜗 : the threshold
그러나 Limits to add가 발생
- adaptation on slower time scales
- possibility for a diversity of firing patterns
- incresed threshold after each spike
- noise
여기서 우리는 abstract current variables인 𝑤를 추가한 미분방정식을 쓸 것이다.

𝑎 : the adaptation coupling parameter
𝑏 : ‘jump’ of the spike-triggered adaptation
𝑘 : 앞 선 spike?
𝑡(f) : the firing time
𝑘=1을 하면

Adaptive Exponential Integrate and Fire (AdEx) : one adaptation variable
- linear + exponential
- adpatation variable
==> various firing patterns

Adaptation : 뉴런에는 spike rate adaptation (or spike frequency adaptation)이라는 메커니즘이 있는데, 이는 일정 기간 동안 활동 전위를 생성하면 발화 속도를 늦춘다.
Bursting : reset value가 high일 때 발생한다. adaptation이 builds up 되고 hyperpolarized potential로의 복귀를 유도할 때까지 reset 후에 spikes가 빠르게 생성되도록 한다.
'Natural Intelligence > Computational Neuroscience' 카테고리의 다른 글
| [Computational Neuroscience] Molecular Dynamics : Periodic Boundary Conditions (0) | 2022.01.19 |
|---|---|
| 계산신경과학 (Computational Neuroscience) (0) | 2022.01.19 |
| [Computational Neuroscience] Leaky Integrate and Fire Model (LIF) (0) | 2021.12.09 |
| [Computational Neuroscience] Dendrites and Synapses (2) (0) | 2021.12.09 |
| [Computational Neuroscience] Dendrites and Synapses (1) (0) | 2021.12.09 |



