728x90
반응형
SMALL
확률 및 확률 분포
|

이산형 확률분포
|
베르누이분포
|
이항분포
|
기하분포
|
다항분포
|
포아송분포
|
연속형 확률분포
|
균일분포
모든 확률변수 X가 균일한 확률을 가지는 확률 분포

정규분포
평균이 u이고, 표준편차가 o인 x의 확률밀도 함수

지수분포
|
t분포
|
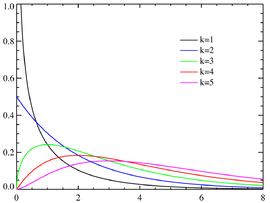
x^2분포 (카이제곱 분포)
|
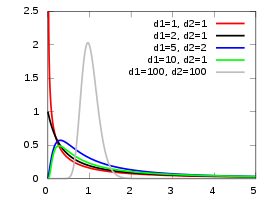
F분포
|
3.3.3.확률 및 확률 분포
+ 표본공간(Sample case) + 어떤 실험을 실시할 때 나타날 수 있는 모든 결과들의 집합 + 사건(event) + 관찰자가 관심이 있는 사건으로 표본공간의 부분 ...
wikidocs.net
728x90
반응형
LIST
'Data-driven Methodology > DS (Data Science)' 카테고리의 다른 글
| [Data Science] 기술통계 (0) | 2022.03.07 |
|---|---|
| [Data Science] 추정과 검정 (0) | 2022.03.07 |
| [Data Science] 기술 통계와 통계적 추론 (0) | 2022.03.07 |
| [Data Science] 통계 분석 (0) | 2022.03.07 |
| [Data Science] 데이터 분석 기법 (0) | 2022.03.07 |



