728x90
반응형
SMALL

추정
|
점추정
|
구간추정
|
가설검정
|
오류
가설 검정의 예
|
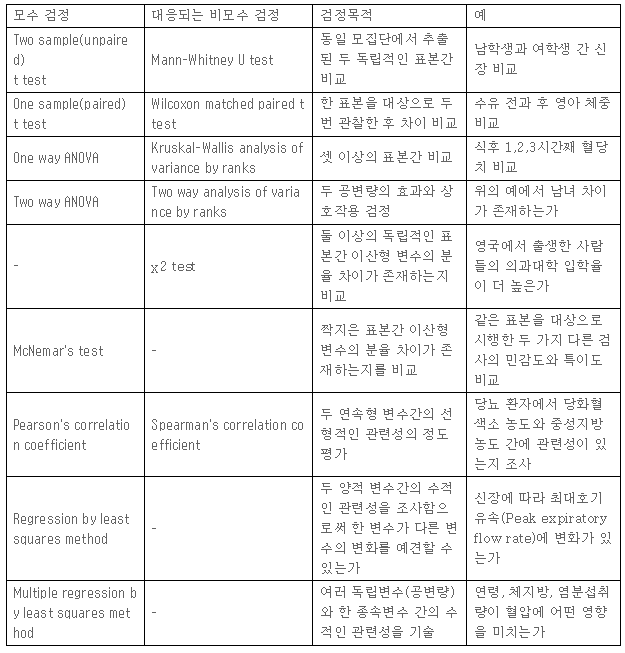
모수 검정과 비모수 검정
통계적 검정에서 모집단의 모수에 대한 검정은 모수적 검정과 비모수적 검정으로 구분
모수 검정
t-검정
|
비모수 검정
|
모수 검정 vs 비모수 검정
3.3.4.추정과 검정
' 카테고리의 다른 글
| [Data Science] 회귀분석 (0) | 2022.03.07 |
|---|---|
| [Data Science] 기술통계 (0) | 2022.03.07 |
| [Data Science] 확률 및 확률 분포 (0) | 2022.03.07 |
| [Data Science] 기술 통계와 통계적 추론 (0) | 2022.03.07 |
| [Data Science] 통계 분석 (0) | 2022.03.07 |



