728x90
반응형
SMALL
gradient 시각화
.
import torch
x = torch.FloatTensor(2, 2)
y = torch.FloatTensor(2, 2)
y.requires_grad_(True) # 향후 gradient를 계산하기 위해 이 tensor가 포함된 모든 연산을 추적(track)한다
z = ( x + y ) + torch.Tensor(2, 2)
print(z)tensor([[2.5832e+30, 2.7510e+36],
[9.7644e+21, 5.9766e+31]], grad_fn=<AddBackward0>)x = torch.FloatTensor(2, 2)
y = torch.FloatTensor(2, 2)
y.requires_grad_(True)
with torch.no_grad(): # 이 연산은 추적하지 않음
z = ( x + y ) + torch.Tensor(2, 2)
print(z)tensor([[-6.9825e+10, 1.2312e-40],
[-2.0730e-26, 1.1014e-40]])w = torch.tensor(2.0, requires_grad=True)
wtensor(2., requires_grad=True)a = w*3 # 3
l = a**2 # 9
print(a)
print(l)tensor(6., grad_fn=<MulBackward0>)
tensor(36., grad_fn=<PowBackward0>)l.backward() # l = (w*3)^2 = 9w^2
print(w.grad) # 미분하면 9 * 2w = 18w
print('l을 w로 미분한 값은 {}'.format(w.grad))tensor(36.)
l을 w로 미분한 값은 36.0w = torch.tensor(1.0, requires_grad=True)
a = w*3 # 3
l = a**2 # 9
l.backward() # l = (w*3)^2 = 9w^2
print(w.grad) # 미분하면 9 * 2w = 18w
print('l을 w로 미분한 값은 {}'.format(w.grad))tensor(18.)
l을 w로 미분한 값은 18.0w = torch.tensor(-1.0, requires_grad=True)
a = w*3 # 3
l = a**2 # 9
l.backward() # l = (w*3)^2 = 9w^2
print(w.grad) # 미분하면 9 * 2w = 18w
print('l을 w로 미분한 값은 {}'.format(w.grad))tensor(-18.)
l을 w로 미분한 값은 -18.0w = torch.tensor(-2.0, requires_grad=True)
a = w*3 # 3
l = a**2 # 9
l.backward() # l = (w*3)^2 = 9w^2
print(w.grad) # 미분하면 9 * 2w = 18w
print('l을 w로 미분한 값은 {}'.format(w.grad))tensor(-36.)
l을 w로 미분한 값은 -36.0
시각화
import matplotlib.pyplot as plt
%matplotlib inline
x = [a for a in range(-5, 6)]
y = [9 * (b * b) for b in range(-5, 6)]
plt.plot(x, y) # 전체 값의 그래프'
for i in [-2, -1, 1, 2]:
plt.plot(i, 9 * (i*i), 'rx')
plt.show()
임의의 x로부터 y가 최소화 되는 위치 찾기 (1)
# x는 param, y는 loss
import matplotlib.pyplot as plt
w = 9
lr = 0.01
x = [a for a in range(-5, 6)]
y = [w * (b * b) for b in range(-5, 6)]
plt.plot(x, y) # 전체 값의 그래프
px = torch.tensor(-2.0)
for i in range(20):
px.requires_grad = True
py = w * (px * px)
plt.plot(float(px), float(py), 'rx')
py.backward()
grad = px.grad
print(grad)
with torch.no_grad():
px = px - grad * lr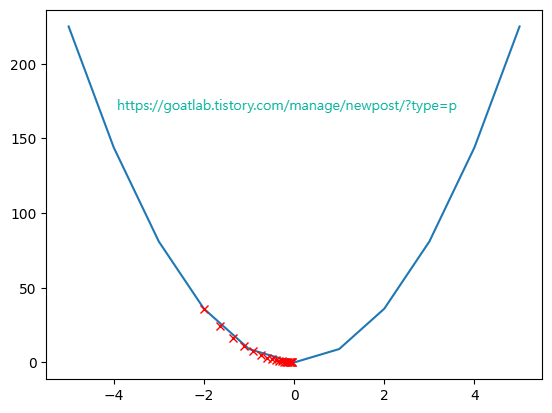
임의의 x로부터 y가 최소화 되는 위치 찾기 (2)
import matplotlib.pyplot as plt
w = 9
lr = 0.01
param = [a for a in range(-5, 6)]
loss = [w * (b * b) for b in range(-5, 6)]
plt.plot(param, loss) # 전체 값의 그래프
p_param = torch.tensor(2.0)
for i in range(20):
p_param.requires_grad = True # param에 대한 연산을 track
p_loss = w * (p_param * p_param) # loss를 계산
plt.plot(float(p_param), float(p_loss), 'rx')
p_loss.backward() # loss에 대한 param의 기울기를 구함
grad = p_param.grad
print(grad)
with torch.no_grad():
p_param = p_param - grad * lr # 기울기의 반대쪽으로 lr만큼 이동. 이 과정은 optimizer가 담당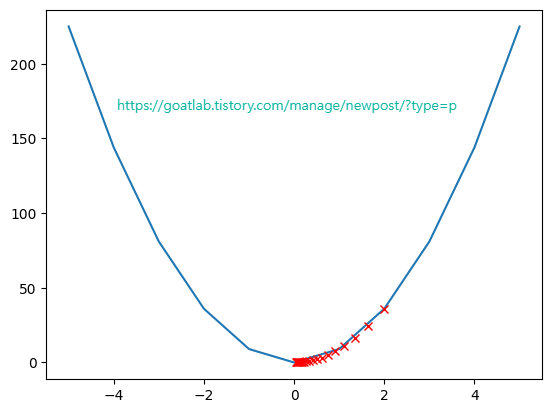
728x90
반응형
LIST
'Python Library > PyTorch' 카테고리의 다른 글
| [PyTorch] AssertionError: Torch not compiled with CUDA enabled (0) | 2024.03.19 |
|---|---|
| [Pytorch] 모델 파라미터 계산 (0) | 2023.05.26 |
| [PyTorch] CNN (0) | 2022.11.21 |
| [PyTorch] CUDA (Compute Unified Device Architecture) (0) | 2022.11.21 |
| [PyTorch] 모델 파라미터 최적화 (0) | 2022.11.21 |



