Direct current (DC)
직류는 일정하게 유지되는 신호이다 (따라서 시간이 지나도 변하지 않음). PSD는 f=0에 완전히 집중되어 있다.
fig, ax = plt.subplots(1,3,figsize=(12,4));
# Direct current(DC)
x = [1 for x in t]
f = [0]
X = [1]
fp,Xp = periodogram(x,fs=sr,detrend=False)
ax[0].axis([0,1,0,1.1])
ax[0].plot(t,x)
ax[1].axis([-1,sr/2,10**-2,2])
ax[1].stem(f,X,use_line_collection=True)
ax[1].set_yscale('log')
ax[2].axis([-1,sr/2,10**-2,2])
ax[2].stem(fp,Xp,use_line_collection=True)
ax[2].set_yscale('log')
DC 신호의 변환은 1 ⋅ δ(0)이고, 즉 모든 전력은 f=0Hz에 집중된다. 따라서 DC 신호는 시간에 따라 변하지 않는 "주기적인" 신호일 뿐이다. 종종 신호의 DC 성분이라고 한다. DC 성분을 제거하는 것은 신호를 ∫f(t)dt=0 (from −∞ to +∞)로 표현한다. 위의 코드에서 fp,Xp = periodogram(x,fs=sr,detrend=False); detrend=False 부품은 주기도에서 DC 성분을 유지한다.
Sinusoid

|
fig, ax = plt.subplots(1,3,figsize=(12,4));
# Sinusoid
x = np.sin(2*np.pi*f_signal*t)
f = [f_signal]
X = [0.5]
fp,Xp = periodogram(x,fs=sr,detrend=False)
ax[0].axis([0,1,-1.1,1.1])
ax[0].plot(t,x)
ax[1].axis([-1,sr/2,10**-2,2])
ax[1].stem(f,X,use_line_collection=True)
ax[1].set_yscale('log')
ax[2].axis([-1,sr/2,10**-2,2])
ax[2].stem(fp,Xp,use_line_collection=True)
ax[2].set_yscale('log')
정현파의 변환은 정현파의 주파수에서 디랙이다. 이것은 PSD에서 표현하는 것이 합산되면 시간 신호를 제공하는 일련의 죄 함수라는 것을 고려하면 다소 분명하다. sin를 분해하는 것은 분명히 sin 자체를 반환할 것이다.
그러나 이상한 것이 있다. 진폭은 0.5뿐이다. 이것은 여기서 절반의 진실만을 보기 때문이다 (문자 그대로). 스펙트럼은 항상 다음에서 실행된다. (from −∞ to +∞ ) 사실 두 가지가 있다. δ 진폭 0.5에서 −fsignal 그리고 fsignal이다. 부정적인 부분이 동일하기 때문에 PSD의 긍정적인 것만 대표하는 것이 오히려 일반적다.
sinc (사인 기수)
sinc 함수는 시간 공간에서 스펙트럼 공간으로 (또는 그 반대로) 전환할 때 자주 발생한다. 다음과 같이 정의된다.

샘플링 함수 또는 매우 구어체로 모양 때문에 멕시코 모자 함수라고도 한다. 그 값을 다음과 같이 정의해야 한다. x=0 나눗셈을 피하기 위함이다. 이것은 정규화된 sinc 함수에 대한 정의이다. 정규화되지 않은 버전을 사용할 것이다. (x=ωt)
이것을 위해 사용할 것이다. -1≤t≤1 "hat"가 t=0에서 중앙에 있기 때문
이다
.
fig, ax = plt.subplots(1,3,figsize=(12,4));
t1 = np.arange(-1,1,1/sr)
x = [np.sin(2*np.pi*f_signal*x)/(2*np.pi*f_signal*x) if x !=0 else 1 for x in t1]
f = [-f_signal/2,f_signal/2,f_signal/2*1.00000000000001,32]
X = [1/f_signal,1/f_signal,0,0]
fp,Xp = periodogram(x,fs=sr,detrend=False,return_onesided=False)
ax[0].axis([-1,1,-1.1,1.1])
ax[0].plot(t1,x)
ax[1].axis([0,sr/2,10**-4,1])
ax[1].plot(f,X)
ax[1].set_yscale('log')
ax[2].axis([0,sr/2,10**-4,1])
ax[2].stem(fp,Xp,use_line_collection=True)
ax[2].set_yscale('log')
변환은 진폭이 있는 1/fsignal 그리고 fsignal의 너비는 정사각형이다 (반은 음의 주파수에 있다). 주기도는 표시에서 상당히 벗어났다. 이는 너비와 진폭이 실제로 샘플링 주파수에 의존하기 때문이다. 흥미롭게도 제곱 함수 (주기적인 구형파가 아닌 단일 구형 펄스)의 변환은 sinc이다.
square wave
푸리에 분해에서 구형파를 살펴본다.
fig, ax = plt.subplots(1,3,figsize=(12,4));
t = np.arange(0,1,1/sr)
x = sps.square(2*np.pi*f_signal*t,0.5)/2;
f = np.arange(1,int(sr/2))*f_signal
X = np.array([(2/n/np.pi)**2*np.abs(np.sin(n*np.pi/2)) for n in range(1,int(sr/2))]);
fp,Xp = periodogram(x,sr)
ax[0].axis([0,1,-0.55,0.55])
ax[0].plot(t,x)
ax[1].axis([0,32,10**-4,1])
ax[1].stem(f,X,use_line_collection=True);
ax[1].set_yscale('log')
ax[2].axis([0,32,10**-4,1])
ax[2].stem(fp,Xp,use_line_collection=True)
ax[2].set_yscale('log')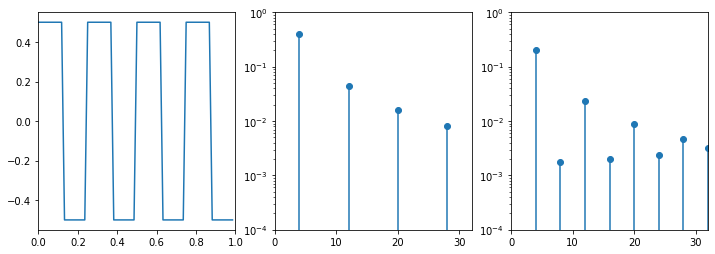
PSD는 δ 진폭으로 2/nπ 모든 홀수 n에 대해 comb이어야 한다. 다시 말하면, 주기도는 이것을 계산하는 데 어려움을 겪는다. 신호가 너무 짧고 샘플링 속도가 너무 낮다.
https://neuro.inf.unibe.ch/AlgorithmsNeuroscience/Tutorial_files/Temporal_vs_Spectral.html
'Brain Engineering > MNE' 카테고리의 다른 글
| Preprocessing : Data Loading (1) (0) | 2022.04.05 |
|---|---|
| Signal Processing : Acquiring Data (0) | 2022.04.05 |
| Signal Processing : Temporal / Spectral Space (1) (0) | 2022.04.05 |
| Signal Processing : Complex Numbers (0) | 2022.04.04 |
| [MNE-Python] fNIRS 장치에서 데이터 가져오기 (2) (0) | 2022.04.04 |



