Nonlinear features
시간 도메인 및 주파수 도메인 기능에 의해 무시되는 일부 정보를 제공하기 때문에 많은 고급 비선형 방법이 HRV 분석에 적용되었다. 그러나 안정적인 결과를 얻기 위해서는 장기간의 데이터 시리즈가 필요한 경우가 많다. 본 연구에서는 단기 HRV 분석에 적합한 일부 비선형 접근법만 사용하였다. 이러한 방법에는 detrended 변동 분석, 멀티스케일 엔트로피, 상호 정보, 자기 상관 계수 및 제로 크로싱 분석이 포함된다.
Detrended fluctuation analysis (DFA)
DFA는 다항식 노이즈를 제거하여 장거리 전력법 상관 관계를 감지하고 조사된 비선형 데이터의 본질적인 변동을 얻을 수 있다. 시계열 x(n) = {x(1), x(2), ⋯, x(N)}의 경우 먼저 평균값을 뺀 후 처리된 계열을 적분한다. 다음으로, 통합된 신호는 동일한 길이 n의 겹치지 않는 세그먼트로 나뉘고 각 세그먼트의 로컬 추세는 최소 제곱법의 도움으로 맞춰진다. 이후 변동 함수는 다음과 같이 계산된다.
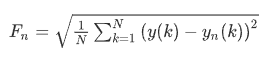
여기서 N은 원래 시퀀스의 총 길이를 나타내고, y(k)는 통합된 신호를 나타내고 yn(k)은 피팅된 로컬 추세를 나타낸다. 위의 프로세스는 F(n)과 n 사이의 관계를 얻기 위해 n의 다른 값에 대해 반복된다. 일반적으로 F(n)은 Fn ∼ nH로 n과 함께 증가한다. 곡선의 기울기인 H이다. log(F(n)) – log(n)은 log–log 평면에 표시되며 DFA 지수로 표시된다. 다른 H는 원래 시퀀스에 고유한 다른 상관 관계를 나타낸다. 연구에서는 H1 과 H2 라고 불리는 두 개의 H 값이 각각 n = 10–30과 30–100 에 대해 계산되었다.
Multiscale entropy (MSE)
MSE는 엔트로피 분석 방법의 범주에 속한다. 거친 입자라고 불리는 프로세스 때문에 생체 신호 분석에서 근사 엔트로피 및 샘플 엔트로피보다 우월함을 나타낸다.
시퀀스 {x(n)}의 경우 스케일 팩터 τ에 해당하는 연속적인 coarse-grained 급수 {yτ(j)}가 처음에 구성되어야 한다. 여기서 . 그런 다음 각 coarse-grained 계열의 샘플 엔트로피와 같은 엔트로피 측정은 원래 시퀀스의 MSE로 계산된다.
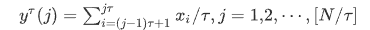
τ 외에 MSE를 계산하기 전에 설정해야 할 두 가지 매개변수가 있다. 임베딩 차원 m과 임계값 r이다. 이것은 coarse-grained 계열의 샘플 엔트로피를 결정하는 중요한 매개변수이다. τ는 3, m 은 2, r은 0.2 * STD로 설정되었으며, 여기서 STD는 {x(n)}이다.
Mutual information (MI)
MI는 두 변수의 상호 통계적 종속성을 정량화하는 효과적인 척도이다. 변수 X와 Y 사이의 MI는 MI(x, y) = H(x) + H(y) − H(x, y)를 통해 결정될 수 있다. 여기서 H (x)와 H (y)는 주변 엔트로피이고 H(x, y)는 X와 Y의 결합 엔트로피이다.
본 논문에서는 각각의 값이 RR과 k만큼 지연된 시간 지연 시퀀스 사이의 MI인 MI 함수 MI (k)를 Long의 방법에 의해 처음에 결정하였다. 그런 다음 비트 감쇠 (BD)와 피크 감쇠 (PD)는 MI 기능의 측정값 으로 도출되었다.

여기서 MI peak1은 2에서 7까지의 k 범위에서 MI(k) 의 첫 번째 극한 최대값을 나타내며 HR에 대한 호흡의 변조를 나타낸다. 해당 범위 내에서 피크가 사라지면 최대값이 사용된다. BD 와 PD 모두 시간 지연에 따라 정보 흐름을 정량화하여 RR 시퀀스의 복잡성을 반영할 수 있다.
Autocorrelation coefficient
Pearson의 RR 간격의 박동간 자기 상관 계수는 REM - NREM 수면 주기동안 다르다. MI와 비교하여 선형 상관 관계만 반영할 수 있지만 특정 생리학적 의미를 내포할 수 있다. 급수 {x(n)}에 대해 자기 상관 함수 r(k)는 다음을 통해 계산할 수 있다.
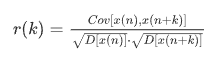
Cov는 공분산이고, 분산에 대한 D(·) 표준이며, x(n + k)는 지연이 k인 시간 지연 계열을 나타낸다. MI와 마찬가지로 RR 시퀀스의 자기 상관 함수 r(k)를 먼저 결정하였다. 그런 다음, BDa 및 PDa 로 표시된 두 개의 기능이 각각 BD 및 PD의 동일한 계산 방식을 통해 추정되었다.
Zero crossing analysis
제로 크로싱 분석은 RR 시퀀스의 진동 특성을 분석하도록 설계되었다. 데이터 시퀀스 {x(n)}을 고려하면 먼저 평균값을 뺀다. 그런 다음 영점 교차점을 찾고 연속적인 영점 교차점 사이의 데이터 수를 ZCI (Zero Crossing Interval)라고 한다. 마지막으로 ZCI의 평균값 (mZCI)과 정규화 표준 편차 (ZCI / mZCI의 표준 편차, nsZCI)를 제로 크로싱 특징으로 추출한다.
여기에서 연구된 RR 레코드의 경우 제로 크로싱 분석 전에 데이터를 4Hz의 샘플링 속도로 리샘플링했다. 다음으로 db6 마더 웨이블릿을 채택하여 리샘플링된 RR 레코드를 레벨 6까지 분해하고 자세한 계수 d1 – d6를 얻는다. 그런 다음 RR 시퀀스의 LF 및 HF 구성 요소의 추정으로 RRl = d5 + d6(0.03125 – 0.125Hz) 및 RRh = d3 + d4(0.125–0.5Hz)를 각각 고려했다. 마지막으로 RR, RRl의 제로 크로싱 기능 및 RRh, 즉 mZCla, nsZCla, mZCl1, nsZCl1, mZClh 및 nsZClh는 위에서 논의된 바와 같이 유도되었다.
HRV features




