Bland–Altman plot

Bland -Altman 플롯 (차이 플롯)은 분석 화학 또는 생물 의학에서 두 가지 다른 분석 간의 일치를 분석하는 데 사용되는 데이터 플로팅 방법이다. 이는 다른 분야에서 알려진 이름인 Tukey 평균차분도와 동일 하지만 J. Martin Bland 및 Douglas G. Altman에 의해 의학 통계 에서 대중화되었다.
현대 임상 실험실에서는 두 가지 정량적 측정 방법 간의 일치를 평가해야 하는 것이 매우 일반적이다. 이 일치 정도를 평가하기 위한 올바른 통계적 접근 방식은 명확하지 않다. 상관 관계 및 회귀 연구가 자주 제안된다. 많은 연구에서 두 가지 측정 방법의 결과 사이의 피어슨 상관 계수 상관 계수 (r)를 일치 지표로 제공한다. 그러나 상관 관계는 차이점이 아닌 하나의 변수와 다른 변수 간의 관계를 연구하며 방법 간의 비교 가능성을 평가하는 방법으로 권장되지 않는다.
1983년 Altman과 Bland (B&A)는 평균 차이를 연구하고 일치 한계를 구성하여 두 정량적 측정 사이의 일치의 정량화에 기초한 대안 분석을 제안했다.
B&A 플롯 분석은 평균 차이 사이의 편향을 평가하고 첫 번째 방법과 비교하여 두 번째 방법의 차이의 95%가 속하는 일치 구간을 추정하는 간단한 방법이다. 데이터는 단위 차이 플롯과 백분율 차이 플롯으로 모두 분석할 수 있다.
B&A 플롯 방법은 합의 간격만 정의할 뿐 해당 한계가 허용 가능한지 여부는 밝히지 않았다. 허용 가능한 한계는 임상적 필요성, 생물학적 고려 사항 또는 기타 목표에 따라 선험적으로 정의되어야 한다.
회귀 분석과 비교
Bland-Altman은 두 측정 기법을 비교하는 데 사용되는 방법이다. 두 가지 방법을 사용하여 수행된 측정값 간의 차이는 방법의 평균에 대해 표시된다. 또는 차이를 평균의 %로 표시할 수 있다. 이것은 신호의 크기가 증가함에 따라 차이의 변동성이 증가하는 경우에 유용하다. 마지막으로, 차이 대신 측정값의 비율을 표시할 수 있다. 이렇게 하면 데이터의 로그 변환이 필요하지 않고 신호의 크기가 증가함에 따라 차이의 변동성이 증가하는 경우에도 유용하다. Bland-Altman은 차이와 평균 간의 관계를 밝히고 체계적인 편향을 찾고 가능한 특이치를 식별하는 데 유용하다. 일관된 치우침이 있으면 새 방법에서 평균 차이를 빼서 치우침을 조정할 수 있다.

예를 들어, 선형 회귀 분석과 Bland-Altman을 사용하여 수행된 plasma clozapine 측정의 두 가지 방법을 비교해 보자. 선형 회귀는 고정 및 비례 편향이 모두 있을 수 있음을 나타낸다. 절편 (0.04–0.12 mg L–1)과 기울기 (0.79–0.94)에 대한 95% CI는 각각 0과 1을 포함하지 않는다. 두 방법으로 측정한 농도 차이를 백분율 또는 절대값으로 표시하면 Bland-Altman은 LC-ED 방법에 대해 약 –0.01mg L–1 또는 –5%의 치우침을 확인할 수 있다.
Bland-Altman 방법의 경우 공식적인 통계 검정이 없으므로 평균 ±1.96 SD 내의 차이가 두 방법이 동등한 것으로 간주될 만큼 충분히 가까운지(이 예제에서는 약 25%) 여부를 결정해야 한다. 데이터는 선형 회귀 분석을 통해 확인된 평균 농도가 증가함에 따라 차이가 증가하는 경향을 보여준다.
Bland-Altman은 일련의 주제에 대해 하나의 단일 방법을 사용하여 여러 측정값을 비교하여 방법의 반복성을 평가하는 데 사용할 수도 있다. 그래프는 방법의 변동성 또는 정밀도가 측정되는 특성의 크기와 관련이 있는지 확인하는 데도 사용할 수 있다. 반복 측정의 경우 동일한 방법이 사용되므로 평균 차이는 0이어야 한다. 따라서, 반복성 계수 (CoR)는 두 측정값 (d2 및 d1) 간의 차이에 대한 SD의 1.96배로 계산할 수 있다.
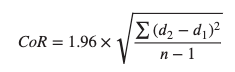
'Statistics' 카테고리의 다른 글
| 피어슨 상관 계수 (Pearson correlation coefficient) (0) | 2023.07.13 |
|---|---|
| 급내 상관 계수 (Intraclass Correlation Coefficients) (0) | 2023.07.12 |
| 유의 확률 (P-Value) (0) | 2023.07.03 |
| Cohen's Kappa (0) | 2023.07.03 |
| 통계학 (Statistics) (0) | 2022.05.19 |



