Euler–Maruyama method
Euler–Maruyama 방법 (Euler 방법)은 확률적 미분 방정식 (SDE) 의 근사 수치 해법이다.
Stochastic differential equation

Euler-Maruyama method : For n = 0, . . . , N − 1

Geometric Brownian motion
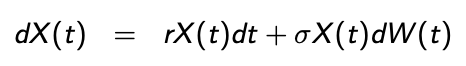
Exact solution


Wiener process

확률 과정 이론에서, 위너 확률 과정 (Wiener stochastic process) 또는 위너 과정은 시간차 △t의 증분의 확률 분포가 평균 0, 분산 △t의 정규 분포를 이루며, 각 증분이 서로 독립이며, 그 궤적이 거의 확실하게 연속적인 연속 시간 확률 과정이다.
https://en.wikipedia.org/wiki/Euler%E2%80%93Maruyama_method
Euler–Maruyama method - Wikipedia
In Itô calculus, the Euler–Maruyama method (also called the Euler method) is a method for the approximate numerical solution of a stochastic differential equation (SDE). It is an extension of the Euler method for ordinary differential equations to stoch
en.wikipedia.org
https://ko.wikipedia.org/wiki/%EC%9C%84%EB%84%88_%ED%99%95%EB%A5%A0_%EA%B3%BC%EC%A0%95
위너 확률 과정 - 위키백과, 우리 모두의 백과사전
확률 과정 이론에서, 위너 확률 과정(Wiener確率過程, 영어: Wiener stochastic process) 또는 위너 과정(Wiener過程)은 시간차 Δ t {\displaystyle \Delta t} 의 증분의 확률 분포가 평균 0, 분산 Δ t {\displaystyle \Delta
ko.wikipedia.org
'Mathematics > Differential equation' 카테고리의 다른 글
| 미분방정식 (Differential equation) (0) | 2022.02.08 |
|---|
