사후 분포 (A Posterior Distribution)
베이지안 추론은 데이터 y를 고려한 후 매개변수 θ의 모든 가능한 값의 확률을 조사하여 도출된다. 하이퍼파라미터 λ가 알려지거나 추정되면 Bayes의 정리를 적용하여 사후 pdf를 얻는다.

분모 p(y | I) = p(y | θ, I) π (θ | λ, I)dθ는 증거로 알려져 있으며 p(θ | y, I) 하나로 통합된다. 결합 분포에서 관측 데이터 y를 제외한 모든 변수를 통합하여 증거를 얻는다. 하이퍼파라미터 λ를 모르는 경우 통합을 통해 이를 제거할 수도 있다.

여기서 π(λ | I)는 λ이다.
주어진 데이터 y에서 θ에 대한 지식을 어떻게 체계적으로 업데이트할 수 있는지 알려준다. 예를 들어, 관측값이 한 번에 하나씩 얻어지면 다음과 같이 사후 분포를 업데이트할 수 있다.

알 수 없는 매개변수가 두 개 이상 있는 경우 θ = (θ1, θ2)이고 θ1과 같은 하나의 구성 요소에만 관심이 있다. 즉각적인 관심은 아니지만 모델에 필요한 미지의 양은 성가신 매개변수로 알려져 있으며 통합에 의해 제거된다.
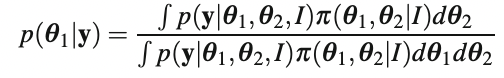
매우 단순해 보이는 형식에도 불구하고 베이지안 통계를 적용하는 것은 어려울 수 있다. 가장 어려운 측면은 다음과 같다.
| (1) 근본적인 물리적 문제의 주요 특징을 효과적으로 포착해야 하는 모델 p(y | θ, I) π (θ, I)의 개발 (2) 사후 분포를 유도하는 데 필요한 필요한 계산. |
표준 확률 분포 함수 (Standard Probability Distribution Functions)

우도 p(θ | y)와 사전 및 사후 분포 p(y | θ, I) 및 p(θ | y, I)에 대한 적절한 모델을 개발할 때 우리는 종종 표준 수학적 분포를 사용한다. 가장 중요한 일변량 분포 f(y)의 목록이다.
Conjugate Priors

공식적으로, 켤레 사전은 우도 함수와 동일한 기능 형태를 갖는 π(θ | I)에 대한 분포 패밀리이다. 결과적으로 켤레 사전을 사용할 때 사후 분포의 기능적 형태는 사전 분포와 동일하다. 따라서 π(θ | I)에 대해 모든 기능적 형태를 선택할 수 있지만 켤레 사전은 가장 큰 수학적 및 계산상의 이점을 누린다.
Non-informative Priors

선험적 분포의 또 다른 부류는 비정보적이거나 "평평한" 선험적 분포이다. 이러한 분포는 본질적으로 실제 분포가 무엇인지에 대한 지식이 없는 상황을 위해 설계되었다. 주어진 변수 θ에 대한 가장 단순한 비정보적 선험적 분포는 π(θ | I)가 1에 비례한다고 가정하는 것이다. 이러한 종류의 고려는 변수의 변화에 불변인 Jeffrey의 선험적 pdf의 개념으로 이어졌다. 다음과 같이 정의된다.
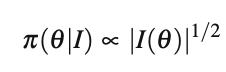
여기서 I(θ) = −E(d2 logp(y | θ) / dθ2)는 Fisher 정보이다. 기타 비정보적 사전 분포는 참조 및 최대 데이터 사전 정보 (MDIP) 분포이다. 표에서는 가우스 분포에 대한 균일 (U), 제프리 (J), 참조 (R) 및 MDIP (M) 비정보 사전을 나열한다.
Missing Data
많은 문제에서 두 종류의 미지수, 즉 매개변수와 하이퍼 매개변수를 다른 한편으로는 누락된 데이터를 구별하는 것이 종종 유용하다. 두 가지 유형의 미지수 사이에 절대적인 구분은 없지만 결측 데이터는 일반적으로 개별 데이터와 직접적으로 관련되며 더 많은 데이터가 관찰될수록 차원이 증가하는 경향이 있다. 반면에 매개변수와 초매개변수는 일반적으로 전체 관측값 모집단을 특성화하며 숫자가 고정되어 있다. 데이터가 주어진 감지 한계 아래에 있기 때문에 데이터가 "누락"되는 경우를 보여준다.
통계 문제에서 결측 데이터 z가 발생하면 L = p(y | θ, I)로 정의되는 "관측 데이터 우도"를 사용하여 추론할 수 있다. 이는 "완전한 데이터 가능성"에서 결측 데이터를 통합하여 얻을 수 있다.
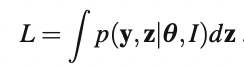
통합을 통해 결측 데이터 문제에 대한 베이지안 분석을 일관성 있게 달성할 수 있다.
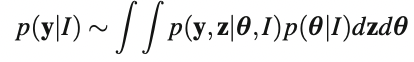
https://link.springer.com/chapter/10.1007/978-3-642-27222-6_12
'Statistics > Bayesian Inference' 카테고리의 다른 글
| [Bayesian Inference] Computation (0) | 2022.03.28 |
|---|---|
| [Bayesian Inference] 모델 선택 (Model Selection) (0) | 2022.03.28 |
| [Bayesian Inference] 가우스 혼합 모델 (Gaussian Mixture Model) (0) | 2022.03.28 |
| [Bayesian Inference] 베이지안 분석 (Bayesian Analysis) (0) | 2022.03.28 |
| 베이지안 추론 (Bayesian Inference) (0) | 2022.03.10 |



